Linear Search in Python
Introduction to Linear Search in Python
Linear search in Python is a simple and straightforward searching algorithm used to find a specific element in a list or array. Enhance your search procedures utilizing the linear search algorithm in Python.
Acquire comprehensive knowledge about step-by-step implementation of linear search in Python, grasp its fundamental principles and diverse applications.
What is Searching Technique?
Searching, in the context of computer science, refers to the process of locating a specific element, value, or data within a collection, such as an array, list, or database.
In Python, searching can be categorized into two main types:
- Linear Search
- Binary Search
What is Linear Search in Python?
Linear search, also referred to as sequential search, is a straightforward algorithmic method used to find a specific element within a collection, such as an array or a list.
Linear search in Python is a simple searching algorithm used to find the presence and location (index) of a specific element within a list or array. It works by sequentially checking each element in the list until a match is found or until the entire list has been examined. If the element is found, the algorithm returns its index; otherwise, it returns a signal (e.g., -1) to indicate that the element is not present in the list.
What is Linear Search with Example?
The following steps are followed for finding element k = 2 from the given array :
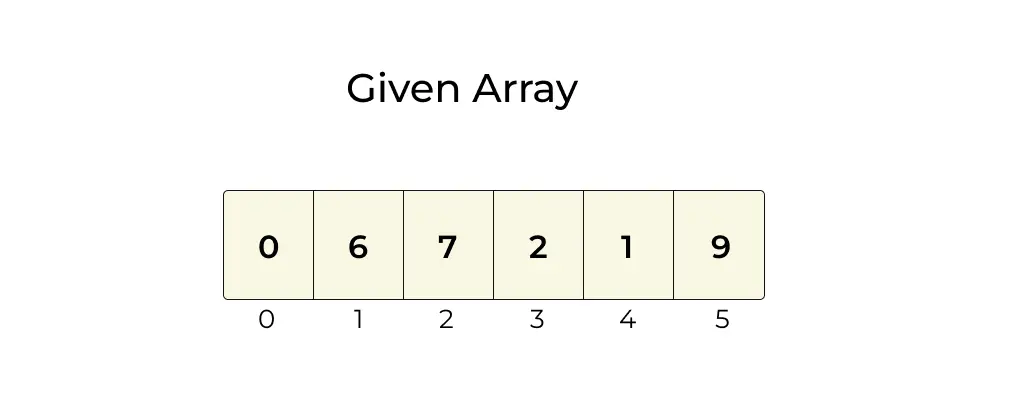
1. Start from the first element and traverse to the last. Here k=2 and each element is x.
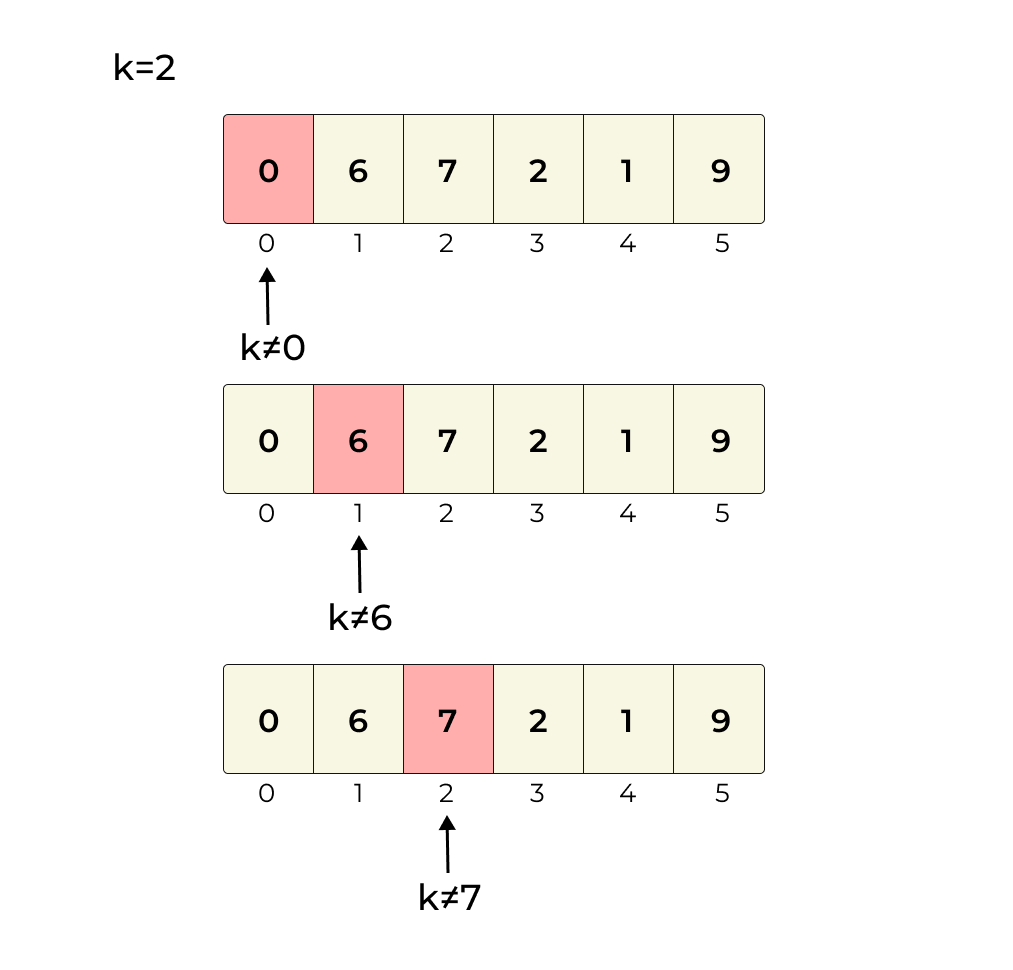
2. If found(k==x); return the index.
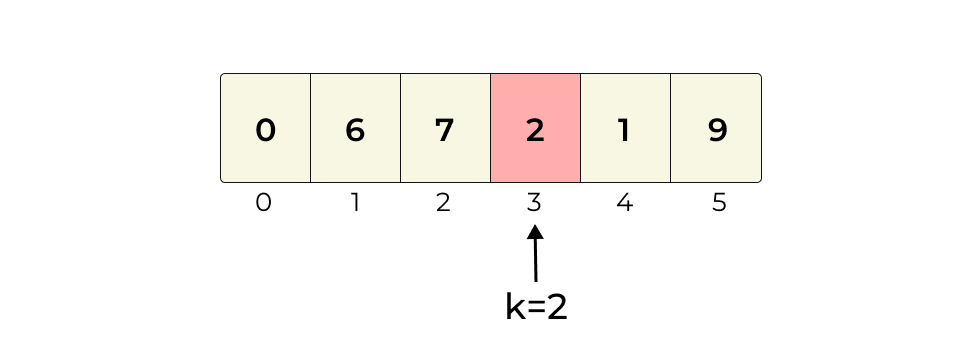
3. Else, not found.

Linear Search Algorithm
Here’s how the Linear Search algorithm works:
Start at the beginning of the collection (usually at index 0).
Compare the target element you’re looking for with the current element in the collection.
If the current element matches the target element, the search is successful, and the algorithm returns the index of the current element.
If there’s no match, move to the next element in the collection and repeat steps 2-3.
Continue this process until you find the target element or reach the end of the collection.
If you reach the end of the collection without finding the target element, the algorithm returns a special value (commonly -1) to indicate that the element was not found.
def linear_search(arr, target):
for index, value in enumerate(arr):
if value == target:
return index
return -1
my_list = [10, 3, 7, 1, 9, 5]
target_value = 7
result = linear_search(my_list, target_value)
if result != -1:
print(f"Target {target_value} found at index {result}")
else:
print("Target not found in the list")
Output: Target 7 found at index 2
Explanation :
- The linear search algorithm checks each element in the list one by one.
- It continues iterating until it finds the target value or reaches the end of the list.
- In this example, the target value 7 is found at index 2.
- The output confirms the correct position of the target in the list.
Time and Space Complexity:
| Complexity Type | Complexity | Explanation |
|---|---|---|
| Time Complexity | O(n) | The algorithm may need to check each element of the list once. |
| Space Complexity | O(1) | Uses only a constant amount of memory regardless of input size. |
Linear Search in Python using List
Run
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
my_list = [10, 4, 7, 2, 8, 5]
target_element = 7
result = linear_search(my_list, target_element)
if result != -1:
print("Element", target_element, "found at index", result)
else:
print("Element", target_element, "not found in the list")
Output: Element 7 found at index 2
Explanation :
- The linear_search function checks each element in the list sequentially.
- It returns the index if the target element is found.
- If the target is not present, it returns -1.
- The example searches for 7 in the list and prints whether it was found or not.
Time and Space Complexity:
| Complexity Type | Complexity | Explanation |
|---|---|---|
| Time Complexity | O(n) | The function may need to scan each element in the list to find the target. |
| Space Complexity | O(1) | Uses constant space as no extra data structures are used. |
Linear Search in Python using for loop
Run
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
my_list = [10, 4, 7, 2, 8, 5]
target_element = 7
result = linear_search(my_list, target_element)
if result != -1:
print("Element", target_element, "found at index", result)
else:
print("Element", target_element, "not found in the list")
Output: Element 7 found at index 2
Explanation :
- The linear_search function uses a for loop to iterate through the list.
- It compares each element with the target and returns the index if found.
- If the target is not found, the function returns -1.
- In this case, the target 7 is found at index 2, and the result is printed.
Time and Space Complexity:
| Complexity Type | Complexity | Explanation |
|---|---|---|
| Time Complexity | O(n) | The function may need to check each element of the list to find the target. |
| Space Complexity | O(1) | No additional space is used; memory usage remains constant. |
Linear Search in Python without using function
Run
my_list = [10, 4, 7, 2, 8, 5]
target_element = 7
found = False
for i in range(len(my_list)):
if my_list[i] == target_element:
found = True
index = i
break
if found:
print("Element", target_element, "found at index", index)
else:
print("Element", target_element, "not found in the list")
Output: Element 7 found at index 2
Explanation :
- The code performs a linear search directly without using a function.
- It uses a for loop to compare each element with the target value 7.
- A boolean flag found is used to track if the target is located during iteration.
- When the target is found, the loop breaks and prints the index; otherwise, it prints a not-found message.
Time and Space Complexity:
| Complexity Type | Complexity | Explanation |
|---|---|---|
| Time Complexity | O(n) | Each element is checked sequentially until the target is found or list ends. |
| Space Complexity | O(1) | Only a few extra variables (`found`, `index`) are used regardless of input size. |
Linear Search in Python using Recursion
Run
def linear_search(arr, target, index=0):
if index >= len(arr):
return -1
if arr[index] == target:
return index
return linear_search(arr, target, index + 1)
my_list = [10, 4, 7, 2, 8, 5]
target_element = 7
result = linear_search(my_list, target_element)
if result != -1:
print("Element", target_element, "found at index", result)
else:
print("Element", target_element, "not found in the list")
Output: Element 7 found at index 2
Explanation :
- The linear_search function uses recursion to search for a target element in a list.
- If the current index exceeds the list length, it returns -1, indicating the element is not found.
- If the element at the current index matches the target, it returns the index.
- Otherwise, the function recursively checks the next index.
- In the given example, it finds the target 7 at index 2 and prints the result.
Time and Space Complexity:
| Complexity Type | Best / Average / Worst Case | Big-O Value |
|---|---|---|
| Time Complexity | Best Case | O(1) |
| Time Complexity | Average Case | O(n) |
| Time Complexity | Worst Case | O(n) |
| Space Complexity | All Cases (due to recursion) | O(n) |
Wrapping up:
The linear search in Python algorithm is well-suited for modestly sized lists (up to 100 elements) due to its examination of every element in pursuit of the sought-after value. In scenarios involving larger lists, such as a list of 10,000 elements with the target value situated at the concluding position, the process becomes time-consuming as each element necessitates comparison.
To expedite results, the binary search algorithm presents an alternative.
The fundamental principles of linear search have been elucidated. In the forthcoming tutorial, we will delve into the second and widely acclaimed searching algorithm known as Binary Search.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
FAQs
Linear Search is a straightforward algorithm that checks each element in a list one by one until it finds the target or reaches the end. It’s widely used for small or unsorted datasets due to its simplicity.
Linear Search has a time complexity of O(n) because it may need to check every element. It uses constant space, making its space complexity O(1).
Unlike Binary Search which requires a sorted list and divides the search range, Linear Search works on unsorted data and scans sequentially. While slower, it’s more flexible and easier to implement.
Linear Search is ideal when the data is small, unsorted, or frequently changing. It’s also useful when ease of implementation is more important than performance.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment