Linear Probing in Hashing

Introduction to Linear Probing in Hashing
In the realm of data structures and algorithms, one of the fundamental concepts is linear probing in hash tables. This technique allows for efficient storage and retrieval of data by handling collisions gracefully.
Let’s jump into the article to know more about Linear Probing in Hashing and also you will get to know about the explaining its inner workings and applications.
Understanding Linear Probing in Hashing
Linear probing in Hashing is a collision resolution method used in hash tables. Collisions occur when two keys produce the same hash value, attempting to map to the same array index. Linear probing deals with these collisions by searching for the next available slot linearly in the array until an empty slot is found.
Linear Probing in Hashing in Python
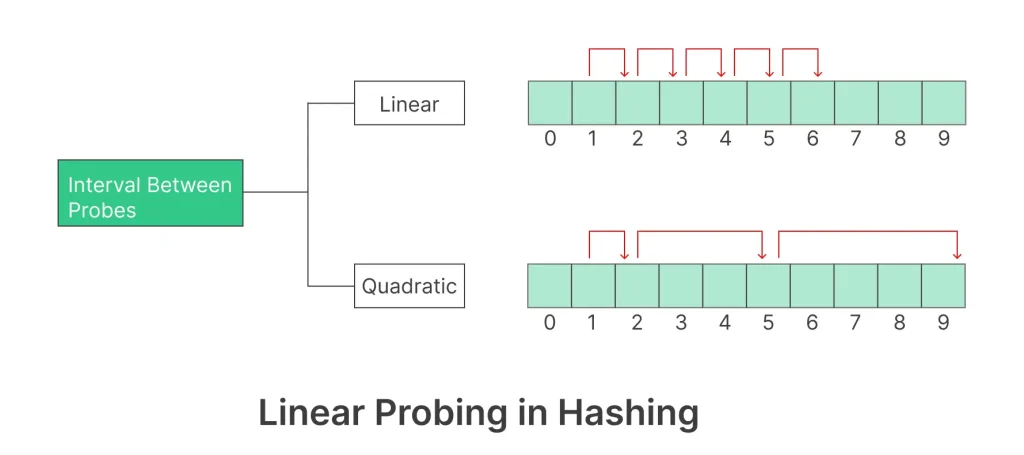
Working of Linear Probing in Hashing
- Calculate the initial hash value for the key.
- If the slot is empty, place the key-value pair there.
- If the slot is occupied, probe linearly by moving to the next slot.
- Repeat steps 2 and 3 until an empty slot is found, and insert the key-value pair there.
Linear Probing in Hashing Example
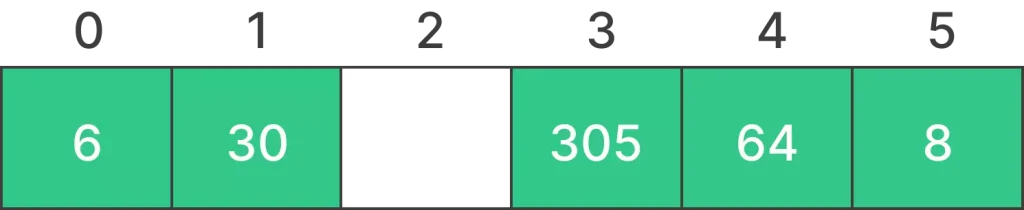
Suppose a hash length of 6 and we want to insert the elements of A.
- A = {30,305,64,8,3}
- h(a) = {1,3,4,5,3}

Step 1 :
According to the function h(a), we have to insert 8 at index 4 and insert 3 at index 3

Step 2 :
- As it is shown in the above figure that index 3 is already occupied by 305, since it is a linear probing and it will repeat all the steps until an empty slot is found, and insert the key-value pair there.
- Now it will follow the previous steps and insert 6 at index 0.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Linear Probing Algorithm Explained
Initialization:
- Create a hash table, which is an array of fixed size, typically a prime number.
- Initialize the hash table with null or empty slots.
Hashing:
- Calculate the initial hash value for the given key using a hash function. The hash function should map the key to an index in the hash table.
Collision Handling:
- If the slot at the calculated index is empty (null or empty), insert the key-value pair into that slot.
Collision Resolution:
- If the slot at the calculated index is occupied by another key-value pair, perform linear probing.
- Linear probing involves probing linearly by moving to the next slot (index + 1) and checking if it’s empty.
- If the next slot is empty, insert the key-value pair there.
- If the next slot is also occupied, continue probing linearly until an empty slot is found.
Search:
- To search for a key, calculate its hash and start probing linearly from the calculated index.
- Continue probing until you find the key or an empty slot, indicating that the key is not in the hash table.
Deletion:
- To delete a key, search for it as described above.
- Once the key is found, mark the slot as deleted or remove the key-value pair.
Performance Optimization:
- To optimize linear probing, consider techniques like double hashing or quadratic probing to reduce clustering and improve overall performance when resolving collisions.
Linear Probing in Hashing Code Example
class HashTable:
def __init__(self, size):
self.size = size
self.keys = [None] * size
self.values = [None] * size
def hash(self, key):
return hash(key) % self.size
def put(self, key, value):
index = self.hash(key)
while self.keys[index] is not None:
if self.keys[index] == key:
self.values[index] = value
return
index = (index + 1) % self.size
self.keys[index] = key
self.values[index] = value
def get(self, key):
index = self.hash(key)
while self.keys[index] is not None:
if self.keys[index] == key:
return self.values[index]
index = (index + 1) % self.size
return None
# Create a hash table with a size of 5
hash_table = HashTable(5)
# Insert key-value pairs
hash_table.put("apple", 5)
hash_table.put("banana", 2)
hash_table.put("cherry", 8)
# Retrieve values
print(hash_table.get("apple")) # Output: 5
print(hash_table.get("banana")) # Output: 2
print(hash_table.get("cherry")) # Output: 8
print(hash_table.get("grape")) # Output: None
Output:
5 2 8 None
Explanation:
- Linear Probing handles collisions by checking the next available index sequentially in the array.
- The hash() function combined with modulo ensures the index stays within the table size.
- The put() method inserts or updates a key by probing until a free or matching slot is found.
- The get() method searches for a key using the same linear probing logic until it’s found or the slot is empty.
- The hash table uses two separate lists for keys and values, and currently doesn’t support deletion.
Time and Space Complexity:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Insertion | O(1) | O(n) |
| Search | O(1) | O(n) |
| Update | O(1) | O(n) |
Advantages of Linear Probing
Final Thoughts:
Linear Probing in Hashing is essential for any programmer and software developer. It’s a versatile tool that can significantly improve the efficiency of your applications, and understanding its inner workings is paramount to its successful implementation. By following the principles outlined in this guide, you’ll be well-equipped to utilize linear probing to your advantage and optimize your data structures.
FAQs
Linear probing is a collision resolution technique in open addressing where, if a hash index is already occupied, the algorithm checks the next available slot linearly. It continues this process until it finds an empty slot.
The main drawback is primary clustering, where a group of consecutive occupied slots builds up, increasing search time. It also leads to performance degradation as the table fills.
When a collision occurs, the algorithm linearly scans the next indices (index + 1, index + 2, etc.) to find a free space. This ensures every element is stored within the table without chaining.
To search, start from the hashed index and linearly check each slot until the element is found or an empty slot is encountered, indicating the element isn’t present.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment