Kruskal’s algorithm In Python
Kruskal’s algorithm Implementation in Python
Kruskal’s algorithm, a fundamental concept in graph theory, provides a straightforward approach to find the minimum spanning tree of a connected graph. This tree ensures the most efficient connection between all the vertices while minimizing the total edge weight.
In this tutorial, we’ll simplify the complexities of Kruskal’s algorithm and guide you through its implementation in Python.
What is Kruskal’s Algorithm?
Kruskal’s algorithm is a greedy algorithm used to find the minimum spanning tree of a connected, undirected graph. In simpler terms, it helps to find the most efficient way to connect all the vertices in a graph while minimizing the total edge weight.
Step by Step working of kruskal’s algorithm :
Below is the illustration of the kruskal’s algorithm :
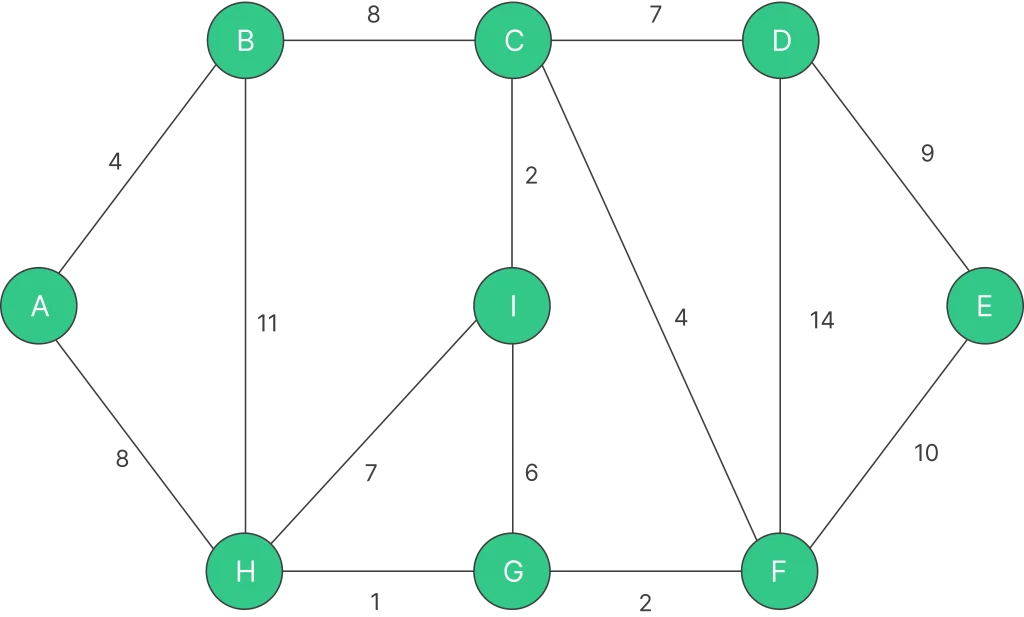
The graph consists of 9 vertices and 14 edges. Therefore, the minimum spanning tree formed will comprise 8 edges, as it connects all 9 vertices with the minimum total weight.
After sorting:
| Weight | Source | Destination |
|---|---|---|
| 1 | H | G |
| 2 | I | C |
| 2 | G | F |
| 4 | A | B |
| 4 | C | F |
| 6 | I | G |
| 7 | C | D |
| 7 | G | I |
| 8 | A | H |
| 8 | B | C |
| 9 | D | E |
| 10 | F | E |
| 11 | B | H |
| 14 | D | F |
Now pick all edges one by one from the sorted list of edges.
Step 1: Pick edge H – G. No cycle is formed, include it.

Step 2: Pick edge I – C. No cycle is formed, include it.
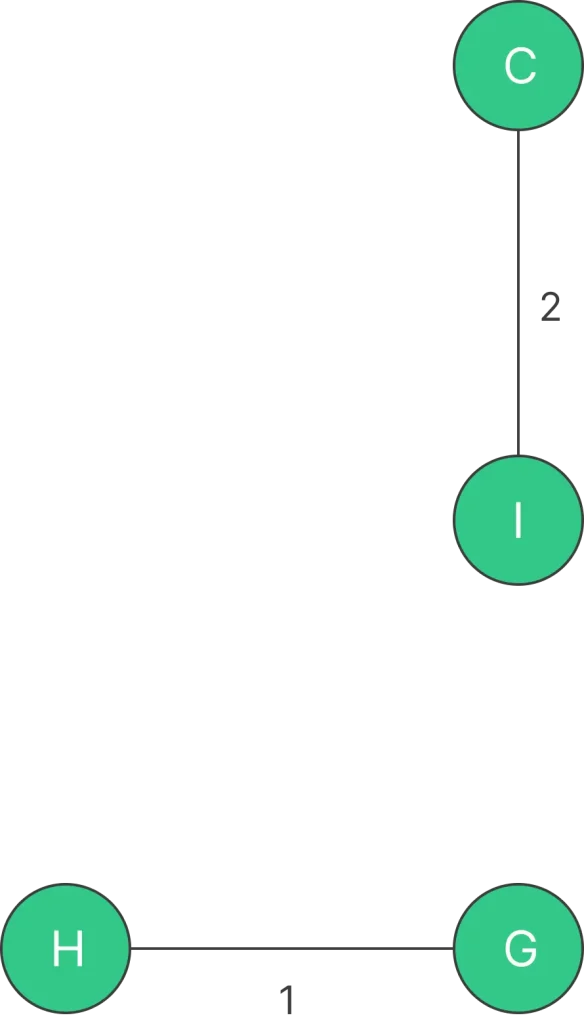
Step 3: Pick edge G – F. No cycle is formed, include it.
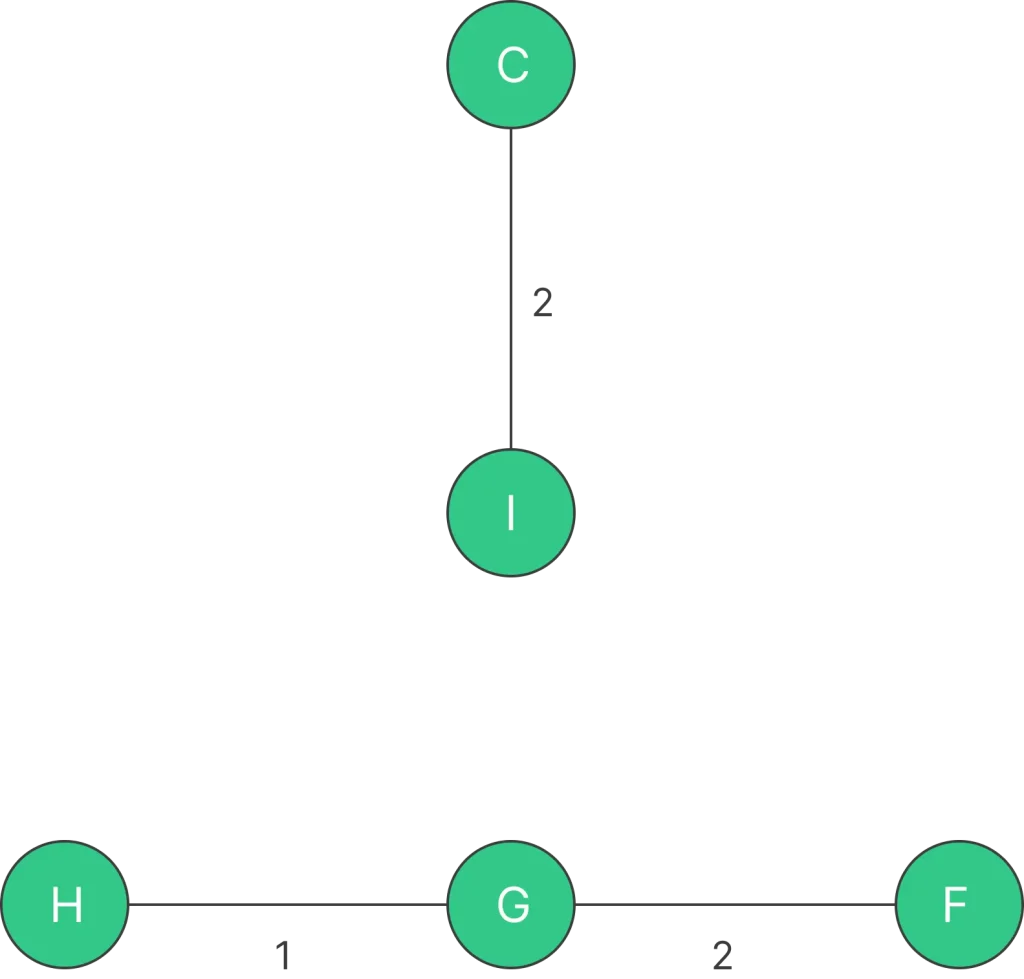
Step 4: Pick edge A – B. No cycle is formed, include it.
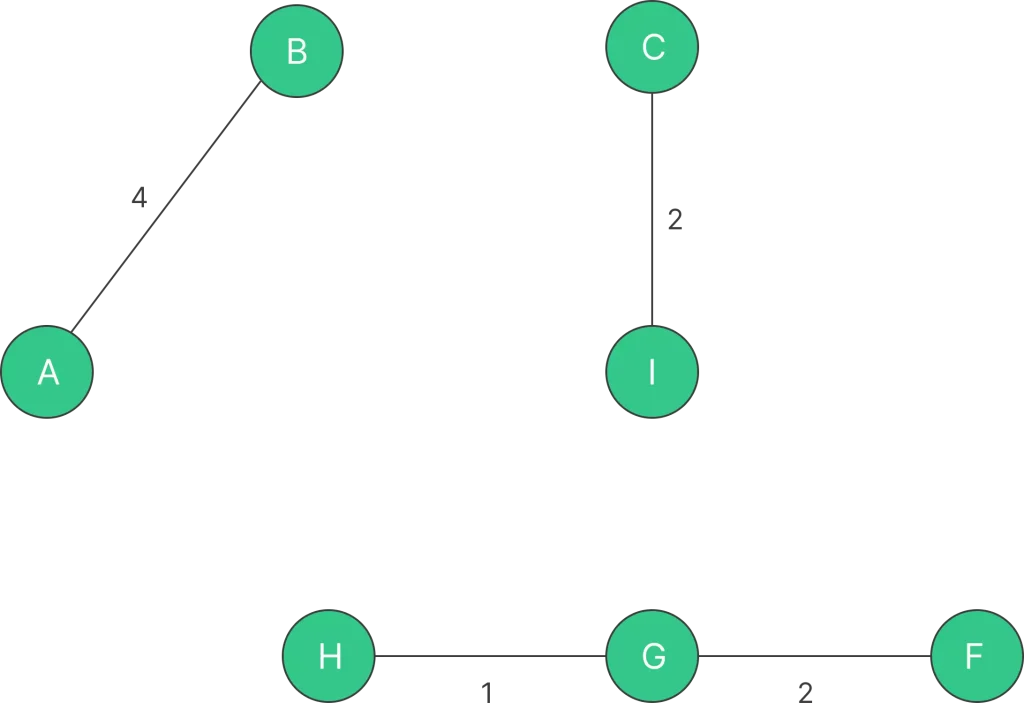
Step 5: Pick edge C – F. No cycle is formed, include it.
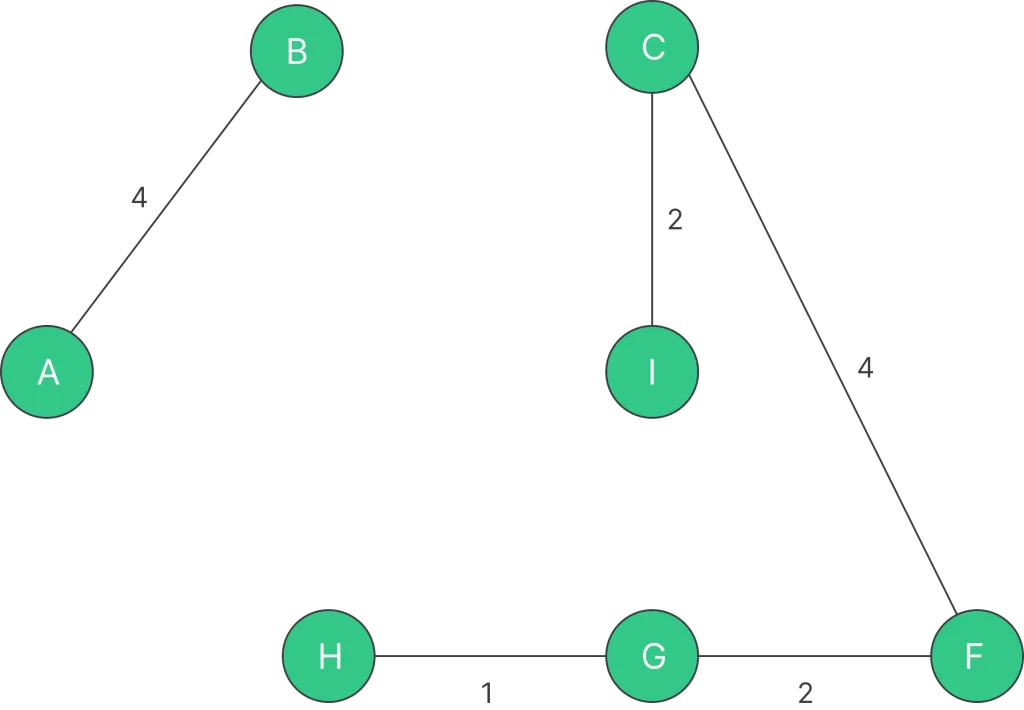
Step 6: Pick edge I – G. Since including this edge results in the cycle, discard it. Pick edge C – D: No cycle is formed, include it.

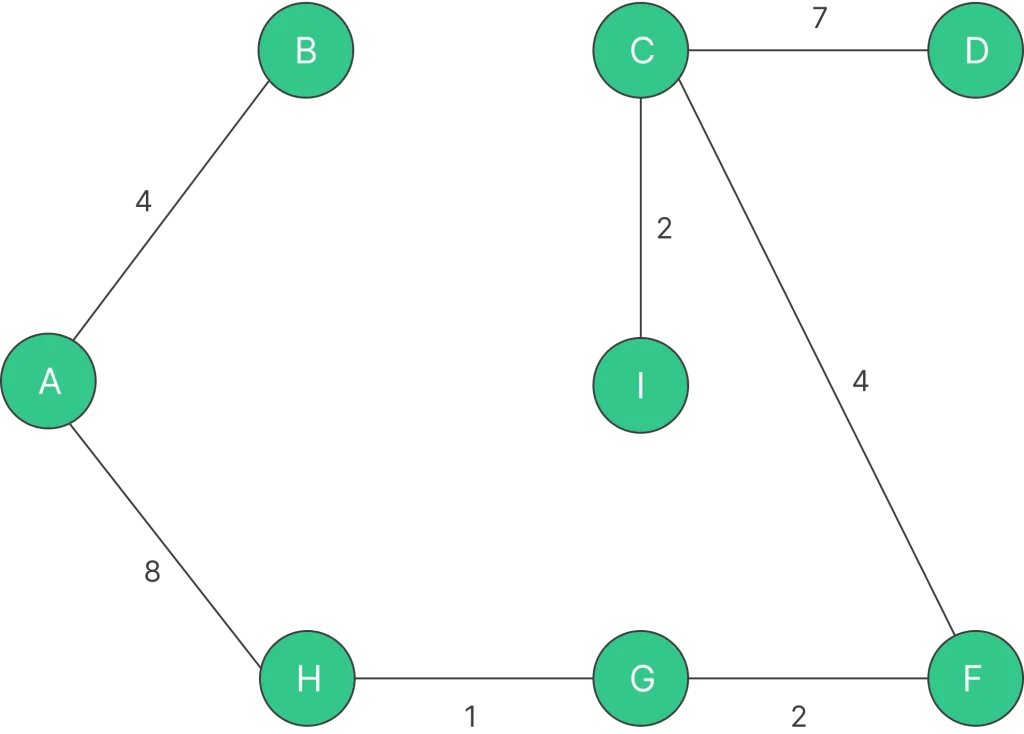
Step 7: Pick edge H – I. Since including this edge results in the cycle, discard it. Pick edge A – H. No cycle is formed, include it.
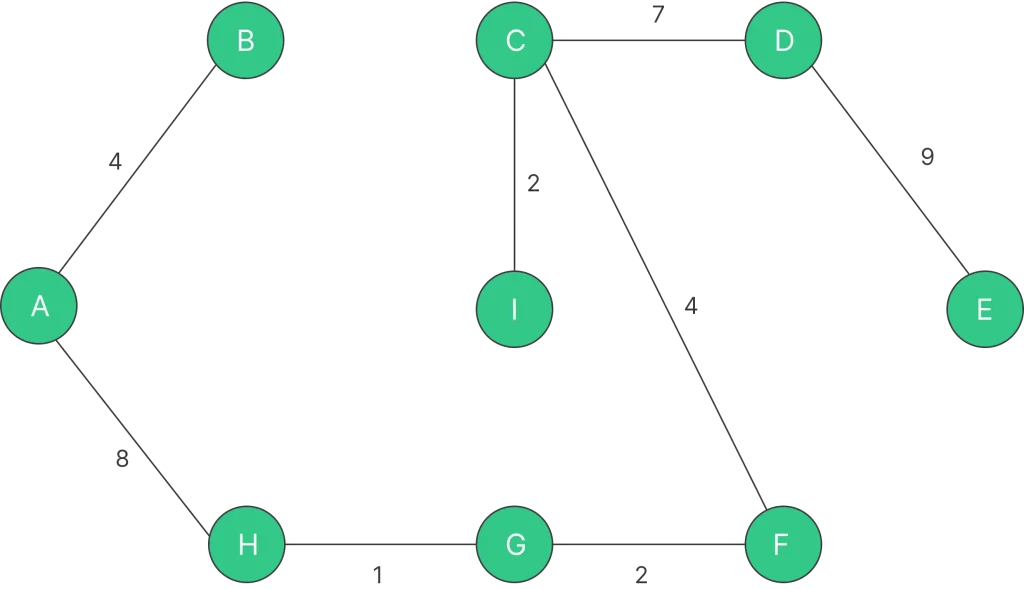
Step 8: Pick edge B – C. Since including this edge results in the cycle, discard it. Pick edge D – E. No cycle is formed, include it.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Kruskal’s Algorithm Pseudocode :
- Initialize an empty list MST.
- Sort all graph edges by weight (ascending).
- Initialize a disjoint set for all vertices.
- For each edge (u, v) in sorted edges:
- If u and v are in different sets:
- Add edge to MST.
- Union the sets of u and v.
- If u and v are in different sets:
- Stop when MST has V – 1 edges.
- Disjoint Set Operations:
- MakeSet(v): Create set for v.
- FindSet(v): Get representative of v’s set.
- UnionSets(u, v): Merge sets of u and v.
Python Implementation for Kruskal’s Algorithm :
class DisjointSet:
def __init__(self, vertices):
self.parent = [i for i in range(vertices)]
self.rank = [0] * vertices
def find(self, node):
if self.parent[node] != node:
self.parent[node] = self.find(self.parent[node])
return self.parent[node]
def union(self, u, v):
rootU = self.find(u)
rootV = self.find(v)
if self.rank[rootU] > self.rank[rootV]:
self.parent[rootV] = rootU
elif self.rank[rootU] < self.rank[rootV]:
self.parent[rootU] = rootV
else:
self.parent[rootV] = rootU
self.rank[rootU] += 1
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = []
def add_edge(self, u, v, weight):
self.graph.append([u, v, weight])
def kruskal(self):
self.graph = sorted(self.graph, key=lambda item: item[2])
mst = []
ds = DisjointSet(self.V)
for edge in self.graph:
u, v, weight = edge
if ds.find(u) != ds.find(v):
mst.append([u, v, weight])
ds.union(u, v)
return mst
# Example usage
g = Graph(4)
g.add_edge(0, 1, 10)
g.add_edge(0, 2, 6)
g.add_edge(0, 3, 5)
g.add_edge(1, 3, 15)
g.add_edge(2, 3, 4)
minimum_spanning_tree = g.kruskal()
print("Edges in the Minimum Spanning Tree:")
for edge in minimum_spanning_tree:
print(edge[0], "-", edge[1], ":", edge[2])
Output:
Edges in the Minimum Spanning Tree: 2 - 3 : 4 0 - 3 : 5 0 - 1 : 10
Explanation:
- Sort Edges by weight to process the lightest first.
- Use Disjoint Set to avoid cycles in MST.
- Path Compression + Union by Rank optimizes find/union operations.
- Add Edge if Safe: Only add if it connects different sets.
- Stop at V-1 edges to complete the MST.
Complexity analysis
| Measure | Complexity | Explanation |
|---|---|---|
| Time | O(E log E) + O(E α(V)) | Sorting edges dominates; DSU operations add almost no extra cost. |
| Space | O(E + V) | Edge list requires O(E) space; the parent and rank arrays in DSU use O(V). |
To wrap it up:
Kruskal’s Algorithm is a greedy technique that finds the minimum spanning tree by selecting the smallest weight edges while avoiding cycles. It’s simple yet powerful, commonly used in solving network optimization problems.
Implementing Kruskal’s Algorithm in Python enhances your grasp of greedy algorithms, graph theory, and data structures like disjoint sets skills crucial for coding interviews and efficient algorithm design.
FAQs
Disjoint sets help efficiently track and merge connected components, preventing cycles in the spanning tree.
No, Kruskal’s algorithm works only for connected graphs. For disconnected graphs, it can produce a minimum spanning forest.
Kruskal’s sorts edges and picks the smallest, while Prim’s grows the MST from one vertex by picking minimum-weight adjacent edges.
The overall time complexity is O(E log E) due to edge sorting and efficient disjoint-set operations.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment