Inorder Traversal of Binary Tree
Introduction to Inorder Traversal
Inorder Traversal of Binary Tree is a versatile technique with applications ranging from organizing data in sorted order to evaluating expressions, parsing code, creating abstract syntax trees, and ensuring the validity of binary trees. Inorder traversal is a fundamental tree traversal algorithm used to visit and process all the nodes of a binary tree. The term “inorder” refers to the specific order in which nodes are visited during this traversal.
Let’s learn more about Inorder Traversal along with its working and implementation.
What is Inorder Traversal of Binary Tree?
An “inorder traversal” is a method of visiting or traversing the nodes of a binary tree, a hierarchical data structure. Specifically, it is a depth-first traversal algorithm that follows the left, root, and right order, which is why it is sometimes also called “left-root-right” traversal.
Inorder Traversal Example
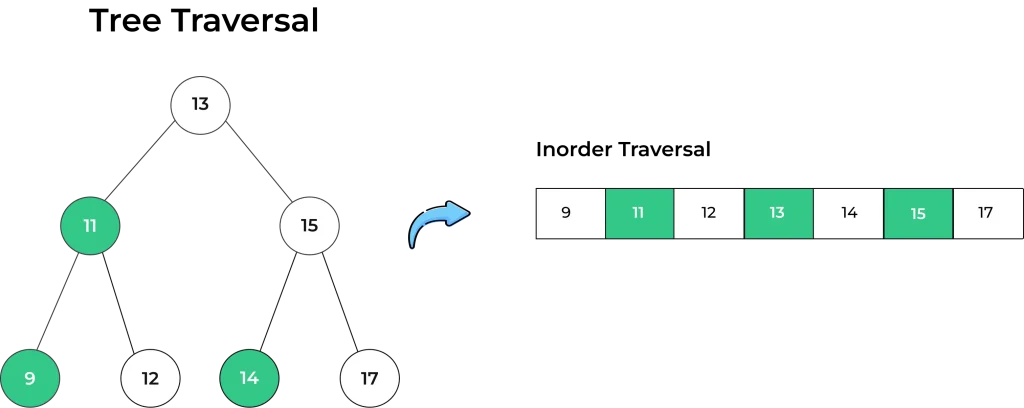
Visualization of Inorder Traversal
In inorder traversal, you visit the nodes in a specific order:
- Traverse the left subtree in a inorder fashion.
- Then, traverse through the root of the binary tree
- And at the last, Traverse the right subtree in a inorder fashion.
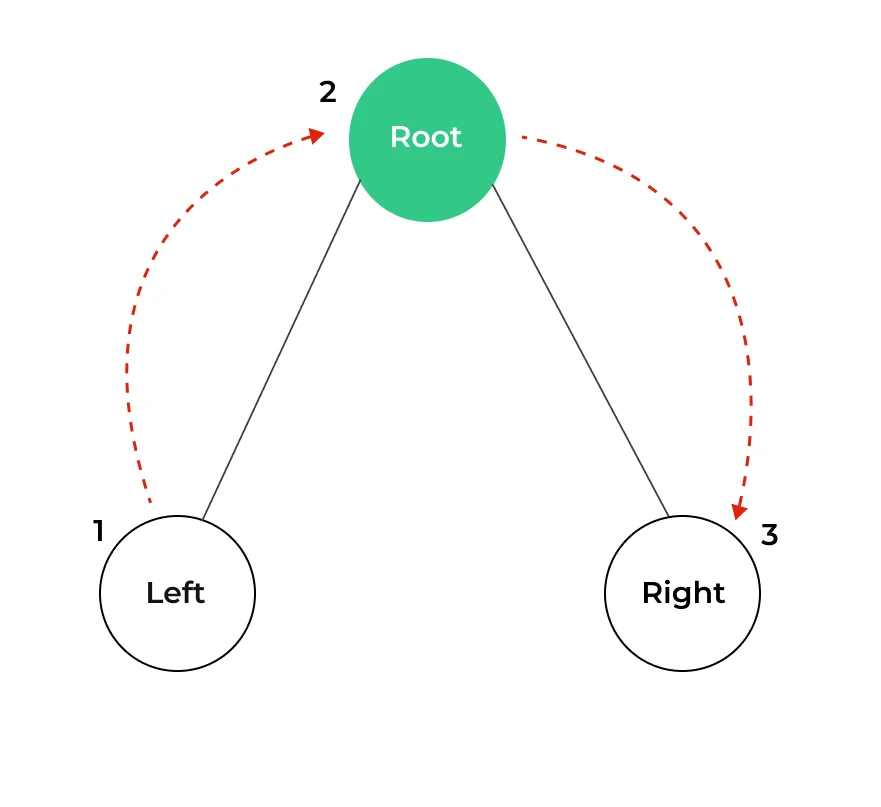
Working of Inorder Traversal of Binary Tree
Consider a binary tree :
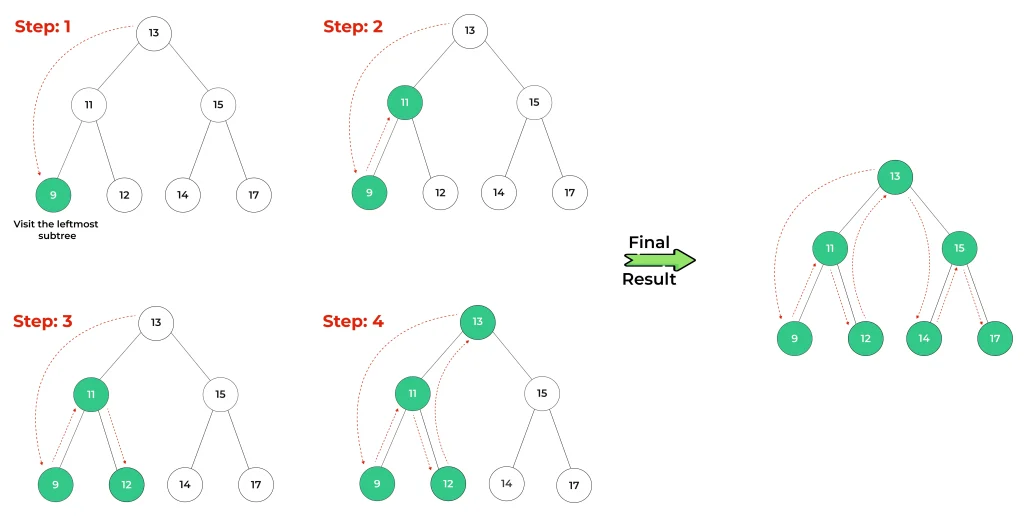
Performing a inorder traversal on this binary tree involves the following steps:
Step 1: Begin from the leftmost subtree.
Step 2: Traverse the root node i.e. node 11.
Step 3: Then traverse through the right subtree of the root node 11 i.e. node 12.
Step 4: Repeat these steps to get the final result.
Pseudocode for Inorder Traversal of Binary Tree
The pseudocode for implementing inorder traversal is as follows:
inorder(node):
if node is not null:
inorder(node.left) // Recursively traverse the left subtree
visit(node) // Visit (or process) the current node
inorder(node.right) // Recursively traverse the right subtree
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Inorder Traversal using Recursive Method
Code :
class TreeNode:
def __init__(self, value):
self.val = value
self.left = None
self.right = None
def inorderTraversal(node):
if node is not None:
# Recursively traverse the left subtree
inorderTraversal(node.left)
# Visit (or process) the current node
print(node.val)
# Recursively traverse the right subtree
inorderTraversal(node.right)
# Construct your binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# Perform the inorder traversal
inorderTraversal(root)
Output :
4 2 5 1 3
Explanation :
The code performs an inorder traversal of a binary tree using a recursive approach. It starts from the leftmost node, visits the current node, and then moves to the right subtree. The output displays the values of the tree’s nodes in ascending order if it’s a binary search tree (BST), or in a specific hierarchical order based on the tree’s structure.
Inorder Traversal using Iterative Method(Using Stack)
class TreeNode:
def __init__(self, value):
self.val = value
self.left = None
self.right = None
def inorderTraversalIterative(root):
stack = []
current = root
while current is not None or stack:
while current is not None:
stack.append(current)
current = current.left # Traverse the left subtree
current = stack.pop()
print(current.val, end=' ') # Print the value with a space
current = current.right # Traverse the right subtree
# Construct your binary tree with different values
root = TreeNode(8)
root.left = TreeNode(3)
root.right = TreeNode(10)
root.left.left = TreeNode(1)
root.left.right = TreeNode(6)
# Perform the inorder traversal
inorderTraversalIterative(root)
Output :
1 3 6 8 10
Explanation :
The code demonstrates an iterative inorder traversal of a binary tree. Starting from the leftmost node, it visits each node, prints the value, and moves to the right subtree. The output displays the node values in ascending order, reflecting the hierarchical structure of the tree with the provided numerical values.
Complexity Analysis of Inorder Traversal of Binary Tree
The time and space complexity analysis for inorder traversal of a binary tree can be summarized as follows:
Time Complexity:
- In the worst case, where the binary tree is skewed, the time complexity of both recursive and iterative inorder traversal is O(n), where n is the number of nodes in the tree. This is because you must visit all nodes once.
- In the average and best cases, for balanced binary trees (e.g., binary search trees), the time complexity is O(n) as well because each node is visited exactly once.
Space Complexity:
- Recursive Inorder Traversal: The space complexity for the recursive approach is determined by the maximum depth of the function call stack, which is proportional to the height of the tree. In the worst case, for a skewed tree, the space complexity is O(n). In a balanced tree, it is O(log n) because the maximum stack depth is logarithmic in terms of the number of nodes.
- Iterative Inorder Traversal: The space complexity for the iterative approach using a stack is also determined by the maximum number of elements stored in the stack, which is proportional to the height of the tree. Similar to the recursive approach, it is O(n) in the worst case (skewed tree) and O(log n) in the best case (balanced tree).
Applications of Inorder Traversal
Following are the applications of Inorder traversal :
To Wrap it up:
In conclusion, Inorder traversal of Binary tree is a valuable technique for exploring the nodes of a binary tree, providing ordered access to the tree’s elements. Whether you’re searching for specific elements in a binary search tree, printing elements in sorted order, or tackling more complex algorithms, understanding and implementing inorder traversal is a fundamental skill for any computer scientist or programmer working with binary trees.
Question 1.
Can Inorder Traversal be Applied to Non-binary Search Trees?
Yes, inorder traversal can be applied to general binary trees. While it doesn’t guarantee sorted order in non-BSTs, it provides a hierarchical order for processing tree elements.
Question 2.
What are Practical Applications of Inorder Traversal?
In addition to searching and sorting, inorder traversal is used in expression evaluation, finding the Kth smallest element, and various tree-related algorithms in computer science.
Question 3.
Can Inorder Traversal Detect Unbalanced Trees?
Inorder traversal can be used to detect whether a binary tree is balanced by calculating the height of its left and right subtrees and checking their difference. Unbalanced trees tend to have significant height differences.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
