Height and Depth of a Binary Tree in Python

Introduction to Height and Depth of a Binary Tree
The height of a tree is a property of the entire tree and measures the longest path from the root to a leaf, while the depth of a node is specific to an individual node and represents its position within the tree in terms of the path from the root. These concepts are essential for understanding and analyzing tree data structures and are fundamental in various algorithms and data manipulation operations.
Let’s jump into the article to know more about Height and Depth of a Tree with its various applications.
Height and Depth of a Tree
Height of a Tree in data structure
The height of a tree is the length of the longest path from the root to any leaf node. It represents how deep the tree goes from top to bottom and is measured in the number of edges or levels.
- It helps determine if the tree is balanced or skewed.
- A balanced tree has a smaller height, typically around log(n).
In balanced trees, operations are fast with O(log n) time.
In unbalanced trees, operations slow down to O(n) time.
Depth of a Tree in data structure
The depth of a node in a tree refers to the length of the path from the root node to that specific node. It measures how many edges or levels are traversed to reach that node from the root.
Depth shows a node’s level in the tree.
Root has depth 0; each lower level increases depth by 1.
Height and Depth of a Tree Example
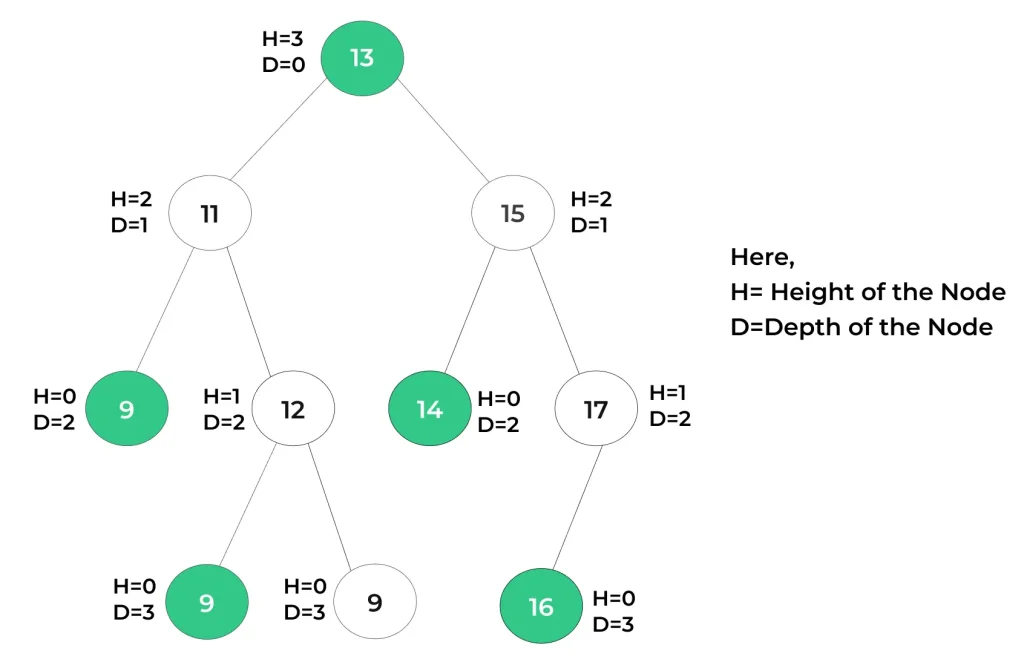
Difference between Height and Depth of a Tree
| Aspect | Height of a Tree | Depth of a Tree |
|---|---|---|
| Definition | The height of a tree is the length of the longest path from the root node to any leaf node in the tree. It measures the overall vertical extent of the tree. | The depth of a node is the length of the path from the root node to that specific node, indicating its position within the tree. |
| Focus | Concerns the entire tree structure. | Focuses on individual nodes within the tree. |
| Minimum Value | The minimum height of any tree is 0, which occurs in a tree with just one node (the root node). | The depth of the root node is always 0, indicating that it is at the top level of the tree. |
| Maximum Value | The maximum height of a tree is equal to the number of levels in the tree. In a perfectly balanced binary tree with ‘n’ nodes, the height is log₂(n). | The maximum depth of a node is equal to the height of the tree, as a node at the deepest level has the same depth as the tree’s height. |
| Use Cases | Important for assessing the overall balance and performance of the tree. | Useful for identifying the relative positions of nodes in the tree and for node-specific operations. |
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Program to find Height of a Tree in Python
Certainly! Here’s a Python code to calculate the height of a binary tree using a recursive approach:
- Recursively compute the height of the left and right subtrees for each node.
- At each node, return the maximum of the two subtree heights plus 1 (to include the current node).
- Base case: If the node is None, return height as 0.
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def tree_height(root):
if root is None:
return 0
left_height = tree_height(root.left)
right_height = tree_height(root.right)
return max(left_height, right_height) + 1
# Create a binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
# Calculate the height of the tree
height = tree_height(root)
print("Height of the tree:", height)
Output :
Height of the tree: 3
- The code calculates the height of a binary tree using recursion.
- It compares the height of left and right subtrees and adds 1 for the current node.
- In the given example, the tree's height is 3, representing the longest path with three edges.
Time and Space Complexity:
- Time Complexity: O(n) — Every node is visited exactly once.
- Space Complexity: O(h) — Due to the recursion stack, where h is the height of the tree (O(log n) for balanced, O(n) for skewed trees).
Program to find Depth of a Tree in Python
Implementation of node depth in a binary tree for printing the output:
- Use recursive DFS to search for the node with the given key, starting from the root.
- At each recursive call, increment the depth and search the left and right subtrees.
- Return the depth when the node is found; if not found in either subtree, return -1.
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
def node_depth(root, key, depth=0):
if root is None:
return -1 # Node not found
if root.value == key:
return depth
left_depth = node_depth(root.left, key, depth + 1)
if left_depth != -1:
return left_depth
right_depth = node_depth(root.right, key, depth + 1)
return right_depth
# Example usage:
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
root.right.left = TreeNode(6)
node_value = 5
depth = node_depth(root, node_value)
if depth != -1:
print("Depth of node " + str(node_value) + ": " + str(depth))
else:
print("Node " + str(node_value) + " not found in the tree.")
Output :
Depth of node 5: 2
- The code uses recursion to traverse a binary tree and calculate the depth of a specific node.
- At each recursive call, it increments the depth until it finds the target node.
- If the node is found, its depth is returned; otherwise, it returns -1 and prints an appropriate message.
- Time Complexity: O(n) — In the worst case, you may need to visit all nodes to find the target.
- Space Complexity: O(h) — Due to recursion stack, where h is the tree height (O(log n) for balanced, O(n) for skewed).
Key Takeaways
- Height of a tree is the longest path from the root node to any leaf node.
- Depth of a node indicates its distance from the root node within the tree.
- Understanding depth helps in efficient node access and managing hierarchical relationships.
FAQs
In Python, height is the longest path from a node to a leaf, while depth is the distance from the root to that node.
You can use recursion to compute both height and depth by traversing the tree and counting the edges accordingly.
It helps improve the efficiency of tree operations like search, insert, and delete by analyzing tree balance and structure.
Yes, especially for leaf nodes in a balanced tree, the height and depth values can be equal depending on node position.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others




Login/Signup to comment