Floor in Binary Search Tree in Python
Exploring the Floor in BST (Binary Search Tree)
When it comes to navigating the intricate world of Binary Search Trees (BSTs), understanding the concept of “floor” is akin to discovering a hidden gem. From the intricacies of the floor operation to its real-world implications, join us in unraveling the magic of BSTs and their floors.
Let’s understand the concept of Floor in BST with its code, complexity and real-world applications.
What is Floor in BST?
In the context of a Binary Search Tree (BST), the “floor” refers to a fundamental concept used to find the largest element in the BST that is less than or equal to a specific target value. In other words, it’s the greatest key in the tree that is not greater than the given value.
Example :
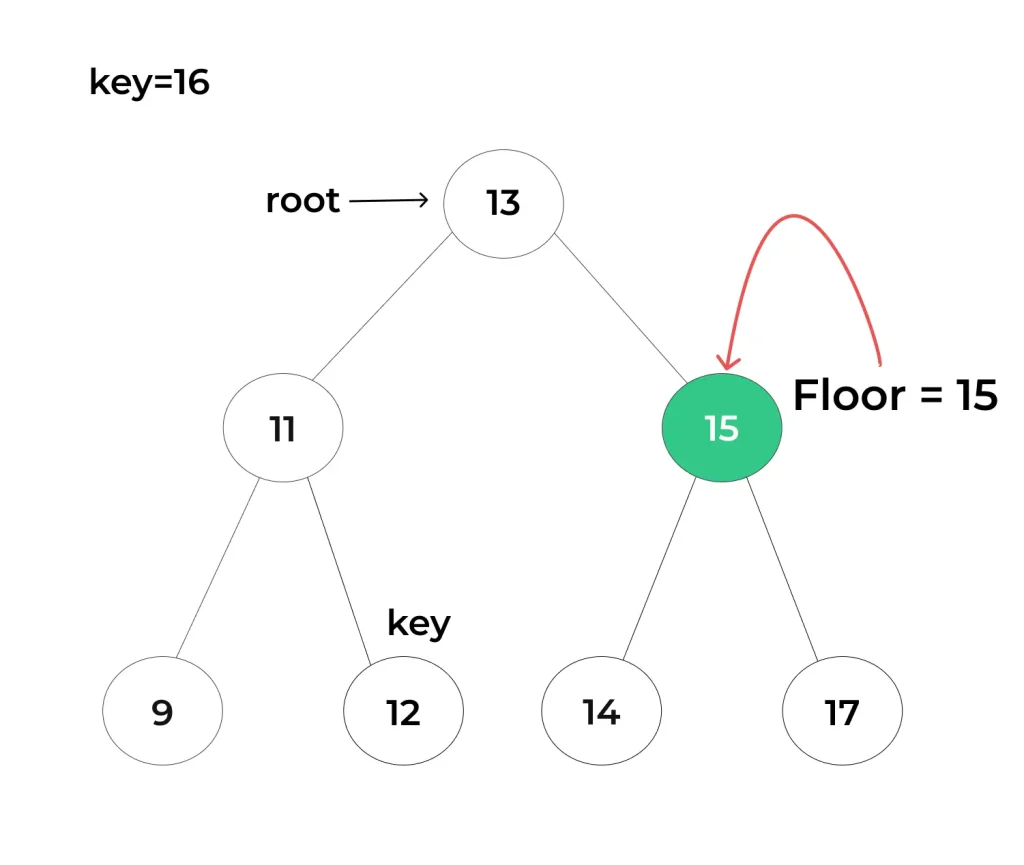
The above example demonstrate the value of Floor value to be “15”(closest value to the target value) as the target value is “16”.
Code for Floor in BST (Binary Search Tree) Using Iterative Solution
Algorithm
- To address this problem, follow these step-by-step instructions:
Start searching from the root node.
If root equals the target key, it is the floor value.
If root > key, check the left subtree.
If root < key, check the right subtree for a value ≤ key.
If no smaller value in right subtree, root is the floor.
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def find_floor(root, target):
floor_value = None
current = root
while current:
if target == current.key:
return current.key
elif target < current.key:
current = current.left
else:
floor_value = current.key
current = current.right
return floor_value
if __name__ == "__main__":
root = TreeNode(50)
root.left = TreeNode(30)
root.right = TreeNode(70)
root.left.left = TreeNode(20)
root.left.right = TreeNode(40)
root.right.left = TreeNode(60)
root.right.right = TreeNode(80)
target_value = 45
result = find_floor(root, target_value)
if result is not None:
print("Floor of", target_value, "is", result, ".")
else:
print("No floor found for", target_value, ".")
Output :
Floor of 45 is 40 .
Explanation
- This Python code finds the floor of a target value in a Binary Search Tree (BST). The “find_floor” function iteratively traverses the tree, updating the floor candidate as it progresses.
- If an exact match is found, it returns the current node’s key as the floor.
- If the target value is smaller, it moves left; if larger, it moves right.
- The final floor candidate is returned as the largest key less than or equal to the target value.
Time and Space Complexity:
- Time Complexity: O(h), where h is the height of the BST (O(log n) for balanced, O(n) for skewed trees).
- Space Complexity: O(h) due to recursive call stack, same as the tree height.
Code for Floor in BST (Binary Search Tree) Using Using Recursion
Algorithm
- Start from the root node.
- If the current node’s key equals the target, return that key.
- If the current node’s key is greater than the target, move to the left subtree.
- If the current node’s key is less than the target, store the current node as a potential floor and move to the right subtree.
- Repeat recursively until the node becomes None.
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def find_floor_recursive(root, target):
if root is None:
return None
if root.key == target:
return root.key
elif root.key > target:
return find_floor_recursive(root.left, target)
else:
floor = find_floor_recursive(root.right, target)
return floor if floor is not None else root.key
# Sample BST
root = TreeNode(10)
root.left = TreeNode(5)
root.right = TreeNode(15)
root.left.left = TreeNode(2)
root.left.right = TreeNode(8)
root.right.left = TreeNode(12)
root.right.right = TreeNode(20)
# Test
target = 13
print("Floor of", target, "is:", find_floor_recursive(root, target))
Output :
Floor of 13 is 12 .
Explanation
We search for the floor of 13.
Since 13 < 15, we go left to 12 (a potential floor).
Since 13 > 12 and there’s no right child, we return 12.
This value is the greatest key less than or equal to 13.
Time and Space Complexity:
Time Complexity: O(h) where h is the height of the BST (log n in balanced tree, n in worst case).
Space Complexity: O(h) due to recursive call stack.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Significance of Finding the Floor in BST
The floor operation in a BST is significant for several reasons:
Data Retrieval: It allows us to efficiently retrieve the largest key that is less than or equal to a given value in a sorted dataset, which can be helpful in search and retrieval operations.
Range Queries: Floor is often used in range queries to find values within a specific range efficiently. It helps identify the starting point of a range.
Interpolation: It plays a role in interpolation algorithms where we estimate a value based on surrounding data points.
Practical Use cases of Floor
The floor operation finds applications in various domains:
Finance: Calculating the floor of stock prices or interest rates can help in financial modeling and risk analysis.
Databases: In databases, floor is useful for range queries, indexing, and data retrieval.
Gaming: In game development, floor values are essential for physics simulations, collision detection, and character movement.
Statistics: It is used in statistical analysis, especially in estimating values within a given range.
Geospatial Data: When dealing with geospatial data, the floor operation aids in locating nearby geographic features or points of interest.
In closing
- The floor in a Binary Search Tree (BST) helps efficiently find the largest key less than or equal to a given value.
- It plays a crucial role in data retrieval, range queries, and estimation tasks.
- Knowing how to implement and use the floor operation in BSTs can significantly improve algorithm performance when working with sorted data.
FAQs
The Floor in Binary Search Tree in Python helps find the closest smaller or equal key to a given target, making approximate lookups fast and efficient.
You can recursively traverse the BST, moving left if the key is smaller and right if it’s larger while storing potential floor values. This ensures the smallest possible greater match is not missed.
The time complexity is O(h), where h is the height of the tree; in balanced BSTs, it becomes O(log n). The space complexity is O(h) for recursion due to the call stack.
It is commonly used in applications like range queries, floor/ceiling value searches in databases, and memory/cache optimization algorithms where nearest-lower values are needed.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others



