Double Hashing in Python

Introduction to Double Hashing in Python
In the world of data structures and algorithms, one powerful technique that often remains overlooked is double hashing. Double hashing is a collision resolution method that proves to be highly efficient when dealing with hash tables.
Let’s jump into the article to know more about Double Hashing in Python and how it can be leveraged to optimize your data storage and retrieval processes.
Understanding Double Hashing in Python
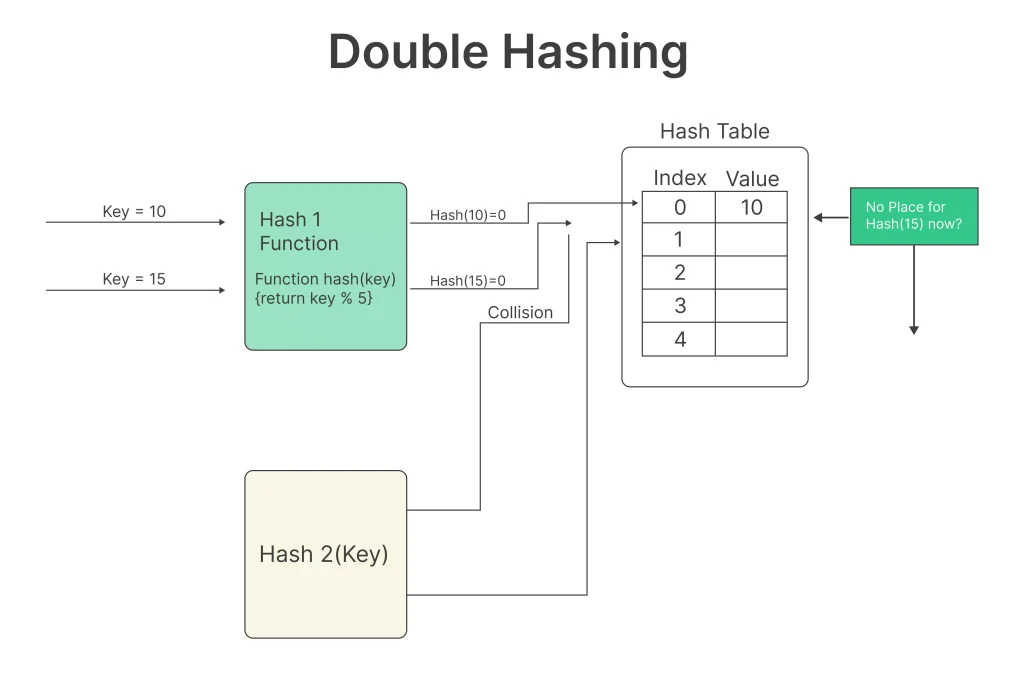
Double hashing is a probing technique used to handle collisions in hash tables. It involves the use of two different hash functions to calculate the next possible location for a key when a collision is encountered. The primary hash function is responsible for calculating the initial hash location, while the secondary hash function guides the search for an available slot in the event of a collision.
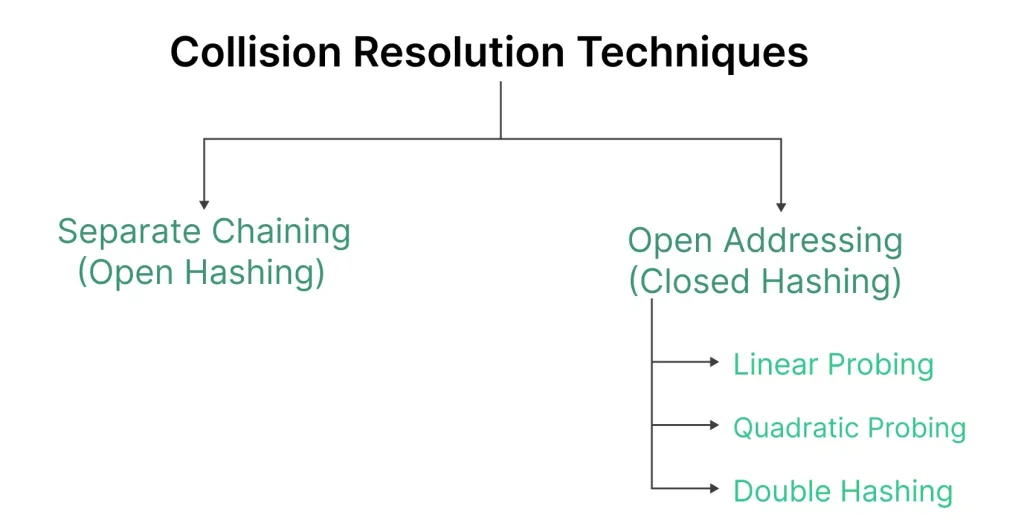
Double Hashing Algorithm
Calculating the Initial Hash:
The primary hash function calculates the initial hash index for a given key. This index is the first position where the key should ideally be stored.
Checking for Collision:
If the calculated index is already occupied by another key, a collision occurs. This is a common occurrence in hash tables due to the limited number of available slots.
Applying Double Hashing:
When a collision happens, the secondary hash function comes into play. It calculates a new index, which is then added to the initial index, creating a new location for the key.
Repeating if Necessary:
If the new index is still occupied, the process repeats until an empty slot is found. The secondary hash function ensures that the search pattern doesn’t become repetitive, increasing the chances of finding an empty slot in a reasonable amount of time.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Python Double Hashing Implementation
# Python code for demonstrating double hashing
class DoubleHashing:
def __init__(self, size):
self.size = size
self.hash_table = [None] * self.size
self.PRIME = 7
def _hash1(self, key):
return key % self.size
def _hash2(self, key):
return self.PRIME - (key % self.PRIME)
def insert(self, key, value):
index = self._hash1(key)
if self.hash_table[index] is None:
self.hash_table[index] = (key, value)
else:
# Collision resolution with double hashing
index2 = self._hash2(key)
i = 1
while True:
new_index = (index + i * index2) % self.size
if self.hash_table[new_index] is None:
self.hash_table[new_index] = (key, value)
break
i += 1
def search(self, key):
index = self._hash1(key)
if self.hash_table[index] is not None and self.hash_table[index][0] == key:
return self.hash_table[index][1]
else:
# Search for the key using double hashing
index2 = self._hash2(key)
i = 1
while True:
new_index = (index + i * index2) % self.size
if self.hash_table[new_index] is not None and self.hash_table[new_index][0] == key:
return self.hash_table[new_index][1]
i += 1
return None
# Create a hash table
hash_table = DoubleHashing(10)
# Insert data
hash_table.insert(5, "Apple")
hash_table.insert(15, "Banana")
hash_table.insert(25, "Cherry")
# Retrieve data
print(hash_table.search(5)) # Output: "Apple"
Output:
Apple
Explanation:
- Implements a hash table using double hashing for collision resolution.
- _hash1(key): Primary hash → key % size.
- _hash2(key): Secondary hash → PRIME – (key % PRIME).
- Insert:
- Try _hash1 index first.
- On collision, use i * _hash2 to find next empty slot.
- Search:
- Check _hash1 index.
- If not found, probe using double hashing until match is found.
- Advantage: Reduces clustering compared to linear probing.
Time and Space Complexity:
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Insertion | O(1) average, O(n) worst | O(n) |
| Search | O(1) average, O(n) worst | O(n) |
FAQs
Double hashing is a collision resolution technique in open addressing where a second hash function calculates the interval between probes. It helps in minimizing clustering and distributes keys more uniformly.
The second hash function is usually designed as R – (key % R), where R is a prime smaller than the table size. This ensures the probing covers all slots in the table efficiently.
Double hashing reduces clustering significantly and offers better performance under high load factors. Unlike linear or quadratic probing, it uses a truly variable step size for probing.
In average case, all operations have O(1) complexity, while in worst-case (high collisions), it can degrade to O(n). Proper hash functions and table size can minimize this risk.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others



