Ceil in BST
Exploring the Ceil in BST (Binary Search Tree)
When it comes to Binary Search Trees (BSTs), the concept of “ceil” holds a vital role in data manipulation and retrieval. Introducing “ceil” — the concept that enables you to find the smallest element greater than or equal to a specified value within a BST.
Let’s understand the importance of the ceil operation, its applications in real-world scenarios, and its impact on algorithms.
What is Ceil in BST?
Ceil refers to a crucial concept used to find the smallest element in the tree that is greater than or equal to a specified target value. It essentially identifies the nearest higher value to the given target within the BST.
Example :
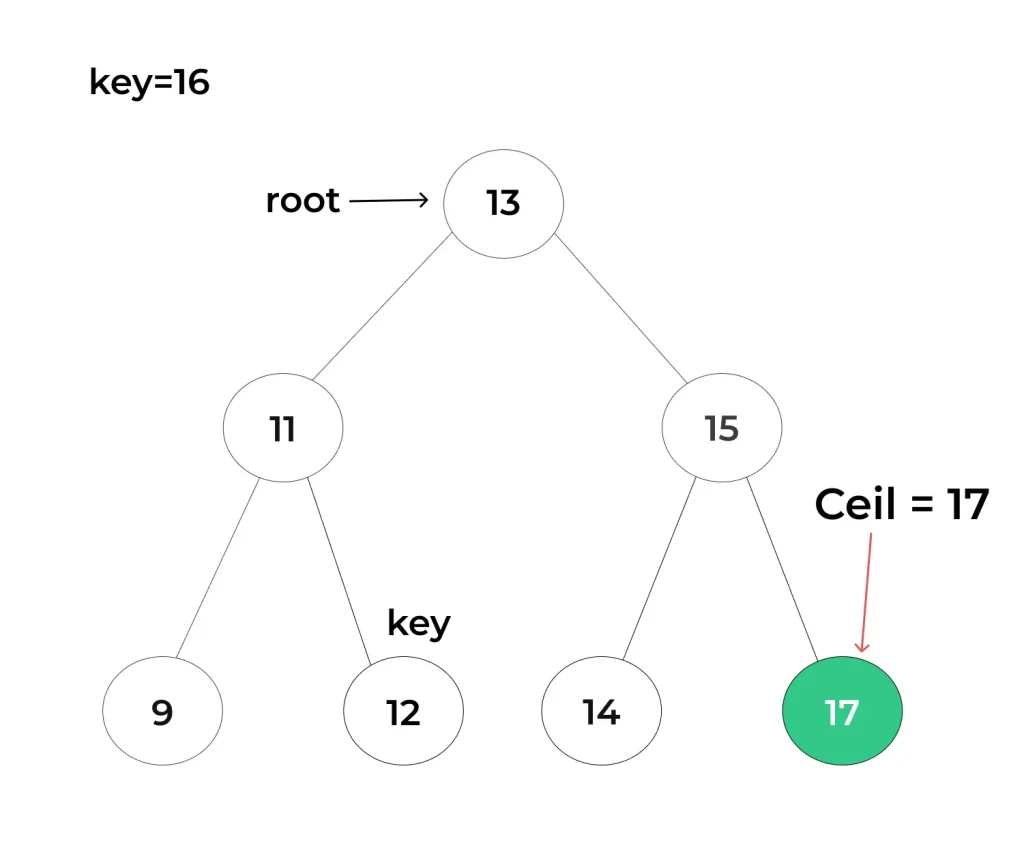
The above example demonstrate the value of Ceil value to be “17”(closest value to the target value) as the target value is “16”.
Algorithm for finding Ceil in BST:
- Start at the root node.
- If the target equals the node’s key, it’s the ceil.
- If the target is less, move to the left (potential smaller ceil).
- If the target is more, move right (update ceil if node’s key ≥ target).
- Repeat until a match is found or traversal ends.
Code for Ceil in BST (Binary Search Tree)
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def find_ceil(root, target):
ceil_value = None
current = root
while current:
if target == current.key:
return current.key
elif target < current.key:
ceil_value = current.key
current = current.left
else:
current = current.right
return ceil_value
# Example usage:
if __name__ == "__main__":
root = TreeNode(50)
root.left = TreeNode(30)
root.right = TreeNode(70)
root.left.left = TreeNode(20)
root.left.right = TreeNode(40)
root.right.left = TreeNode(60)
root.right.right = TreeNode(80)
target_value = 45
result = find_ceil(root, target_value)
if result is not None:
print("Ceil of", target_value, "is", result, ".")
else:
print("No ceil found for", target_value, ".")
Output :
Ceil of 45 is 50 .
Explanation:
- This Python code efficiently determines the ceil of a target value (45) in a BST.
- The “find_ceil” function iteratively traverses the tree, updating the ceil candidate as it progresses.
- If an exact match is found, it returns the current node’s key as the ceil.
- If the target value is smaller, it explores the left subtree, and if it’s larger, it moves to the right subtree.
- The final ceil candidate represents the smallest key greater than or equal to the target value.
Time and Space Complexity:
- Time Complexity:
- O(h) → h is the height of the BST
- O(log n) for balanced BST
- O(n) for skewed BST
- Space Complexity:
- O(1) → uses constant space (no recursion or extra data structures)
More Example on Ceil in BST
Code:
class TreeNode:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
def find_ceil(root, target):
ceil_value = None
current = root
while current:
if target == current.key:
return current.key
elif target < current.key:
ceil_value = current.key
current = current.left
else:
current = current.right
return ceil_value
# Example usage:
if __name__ == "__main__":
root = TreeNode(70)
root.left = TreeNode(40)
root.right = TreeNode(90)
root.left.left = TreeNode(20)
root.left.right = TreeNode(60)
root.right.left = TreeNode(80)
root.right.right = TreeNode(100)
target_value = 55
result = find_ceil(root, target_value)
if result is not None:
print("Ceil of", target_value, "is", result, ".")
else:
print("No ceil found for", target_value, ".")
Output :
Ceil of 55 is 60 .
Explanation
- This Python code effectively calculates the ceil of the target value 55 in a BST.
- The “find_ceil” function iterates through the tree, updating the ceil candidate as it proceeds.
- When an exact match isn’t found, it explores the left or right subtree, depending on the comparison with the current node’s key.
- The final ceil candidate represents the smallest key greater than or equal to the target value.
Time and Space Complexity:
- Time Complexity:
- O(h) → where h is the height of the BST
- O(log n) for balanced BST
- O(n) for skewed BST
- Space Complexity:
- O(1) → constant space, no recursion or extra memory used
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Significance of Finding the Ceil in BST
Discovering the ceil in a BST is essential for various reasons:
Data Retrieval: It allows you to efficiently retrieve the smallest key that is greater than or equal to a given value in a sorted dataset.
Range Queries: Ceil is commonly used in range queries to identify the ending point of a range efficiently.
Interpolation: In data analysis and interpolation algorithms, ceil values assist in estimating values between known data points.
Practical Use cases of Ceil
The ceil operation finds applications in diverse fields:
Finance: Calculating the ceil of stock prices or interest rates aids in financial modeling and analysis.
Databases: Databases use ceil for range queries, indexing, and efficient data retrieval.
Game Development: In game development, ceil values are crucial for collision detection, physics simulations, and character movement.
Statistics: Ceil is employed in statistical analysis, especially when estimating values within a specific range.
Geospatial Data: In geospatial data analysis, finding the ceil helps identify the closest geographic features or points of interest.
To wrap it up:
Understanding the ceil concept in Binary Search Trees is paramount for efficiently locating the smallest key greater than or equal to a target value. Its significance spans across data retrieval, range queries, and estimation tasks in a wide array of applications. As you delve into the world of BSTs and their ceils, you unlock the power to optimize algorithms and make informed decisions based on sorted data.
FAQs
The ceil of a given key in a BST is the smallest key in the tree that is greater than or equal to the target value. It helps in range queries and estimation tasks using sorted tree data.
To find the ceil, start at the root and move left if the key is smaller, while tracking potential ceil values. The time complexity is O(h) where h is the height of the BST.
The floor is the largest value ≤ target, while the ceil is the smallest value ≥ target. Both rely on BST properties for efficient lookup without full traversal.
Yes, if all node values are less than the target, the ceil doesn’t exist and the result is None. This typically happens when the target is greater than the maximum value in the tree.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others



