Binary Search Tree in Data Structure
Introduction to Binary Search Tree
A Binary Search Tree (BST) is a hierarchical data structure where each node’s left subtree contains values less than the node, and the right subtree contains values greater than the node, enabling efficient search and traversal operations.
It is a type of binary tree where each node has at most two children, often referred to as the left child and the right child. BSTs are organized in a hierarchical manner, with nodes containing data values.
Why Binary Search Tree(BST)?
Binary Search Trees (BSTs) are a cornerstone of computer science and data structures for their efficiency and versatility. Their unique ordering principle allows for rapid searching, insertion, and deletion of data, making them invaluable for tasks that require data organization and retrieval.
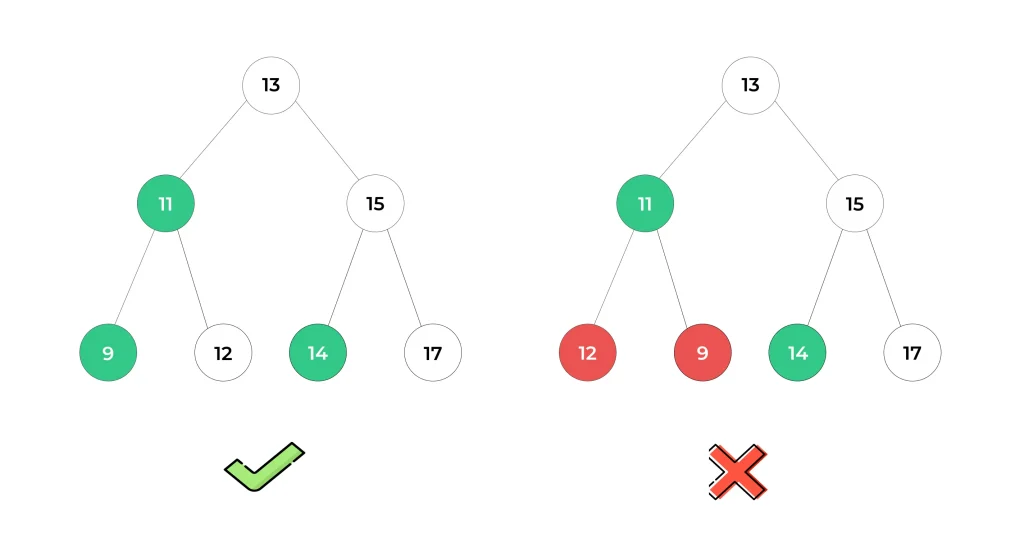
Property of Binary Search Tree(BST)
What distinguishes a Binary Search Tree (BST) from a standard binary tree are the following characteristics:
- The left subtree contains nodes with values less than the root node.
- The right subtree contains nodes with values greater than the root node.
- Each subtree, whether left or right, also adheres to these two properties, thus forming a BST structure.
Algorithm for Binary Search Tree(BST)
If node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;
Important Points:
- The node’s left subtree contains a key that is either less than or equal to the key of its parent node.
- The node’s right subtree contains a key that is either greater than or equal to the key of its parent node.
Implementation of Binary Search Tree(BST)
class TreeNode:
def __init__(self, key):
self.val = key
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, key):
# If the tree is empty, create a new root node
if not self.root:
self.root = TreeNode(key)
else:
self._insert_recursive(self.root, key)
def _insert_recursive(self, current_node, key):
# Recursive function to insert a key into the tree
if key < current_node.val: if current_node.left is None: current_node.left = TreeNode(key) else: self._insert_recursive(current_node.left, key) elif key > current_node.val:
if current_node.right is None:
current_node.right = TreeNode(key)
else:
self._insert_recursive(current_node.right, key)
def search(self, key):
return self._search_recursive(self.root, key)
def _search_recursive(self, current_node, key):
# Recursive function to search for a key in the tree
if current_node is None:
return False
if current_node.val == key:
return True
elif key < current_node.val:
return self._search_recursive(current_node.left, key)
else:
return self._search_recursive(current_node.right, key)
def inorder_traversal(self):
return self._inorder_traversal_recursive(self.root)
def _inorder_traversal_recursive(self, current_node):
# Recursive function for in-order traversal (left-root-right)
result = []
if current_node:
result += self._inorder_traversal_recursive(current_node.left)
result.append(current_node.val)
result += self._inorder_traversal_recursive(current_node.right)
return result
# Example usage:
if __name__ == "__main__":
bst = BinarySearchTree()
bst.insert(50)
bst.insert(30)
bst.insert(70)
bst.insert(20)
bst.insert(40)
# In-order traversal should return elements in ascending order
inorder_result = bst.inorder_traversal()
print("In-order traversal:", inorder_result) # Output: [20, 30, 40, 50, 70]
key_to_search = 40
if bst.search(key_to_search):
print(str(key_to_search) + " found in the BST.")
else:
print(str(key_to_search) + " not found in the BST.")
Output :
In-order traversal: [20, 30, 40, 50, 70] 40 found in the BST.
Explanation
The in-order traversal of the BST [20, 30, 40, 50, 70] is printed, which represents the elements in ascending order. The code then searches for the key 40 in the BST and successfully finds it, so it prints “40 found in the BST.”
Operations in Binary Search Tree(BST)
- Insertion:
- Add a new node with a given key into the BST while maintaining the BST property.
- Python code for insertion:
def insert(self, key):
if not self.root:
self.root = TreeNode(key)
else:
self._insert_recursive(self.root, key)
- Search:
- Check if a specific key exists in the BST.
- Python code for search:
def search(self, key):
return self._search_recursive(self.root, key)
- Deletion:
- Remove a node with a specific key from the BST while preserving the BST structure.
- Python code for deletion:
def delete(self, key):
self.root = self._delete_recursive(self.root, key)
- In-order Traversal:
- Visit all nodes in the BST in ascending order (left-root-right).
- Python code for in-order traversal:
def inorder_traversal(self):
return self._inorder_traversal_recursive(self.root)
- Pre-order Traversal:
- Visit nodes in the order root-left-right.
- Python code for pre-order traversal:
def preorder_traversal(self):
return self._preorder_traversal_recursive(self.root)
- Post-order Traversal:
- Visit nodes in the order left-right-root.
- Python code for post-order traversal:
def postorder_traversal(self):
return self._postorder_traversal_recursive(self.root)
Time and Space Complexity for Binary Search Tree in Python
The time and space complexities of Binary Search Trees (BSTs) in Python depend on various factors, including the structure of the tree, the specific operation being performed, and whether the tree is balanced or unbalanced. Here are the average-case complexities for some common BST operations:
Insertion:
- Average Time Complexity: O(log n) for a balanced BST, where “n” is the number of nodes in the tree.
- Worst-case Time Complexity: O(n) for an unbalanced tree.
- Space Complexity: O(log n) for recursive call stack in a balanced BST; O(n) in an unbalanced BST.
Search:
- Average Time Complexity: O(log n) for a balanced BST.
- Worst-case Time Complexity: O(n) for an unbalanced tree.
- Space Complexity: O(log n) for recursive call stack in a balanced BST; O(n) in an unbalanced BST.
Deletion:
- Average Time Complexity: O(log n) for a balanced BST.
- Worst-case Time Complexity: O(n) for an unbalanced tree.
- Space Complexity: O(log n) for recursive call stack in a balanced BST; O(n) in an unbalanced BST.
To wrap it up:
In conclusion, the Binary Search Tree (BST) stands as a fundamental and powerful data structure within the realm of computer science. Its elegant hierarchical organization, guided by the principles of left-subtree values being less and right-subtree values being greater than the root node, enables efficient operations for data insertion, retrieval, and deletion.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Question 1.
What happens if a Binary Search Tree becomes unbalanced?
If a BST becomes highly unbalanced (resembling a linked list), the time complexities for operations degrade to O(n), which can result in poor performance. Self-balancing BST variants like AVL trees and Red-Black trees are used to maintain balance.
Question 2.
How can I insert data into a Binary Search Tree?
To insert data into a BST, compare the value with the root node. If it’s less, go left; if greater, go right. Repeat this process until an empty spot is found, then insert the new node.
Question 3.
What is the in-order traversal of a Binary Search Tree?
In-order traversal visits nodes in ascending order (left-root-right) and is often used to retrieve data from a BST in sorted order.
Question 4.
Are Binary Search Trees used in real-world applications?
Yes, BSTs are widely used in various applications, including databases (for indexing), symbol tables, compilers (for parsing and symbol tables), and more.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
