Power of a Number using Recursion in C++

October 12, 2022

Power of a Number using Recursion in C++

 

Here, in this page we will discuss the program to find power of a number using recursion in C++ programming language. We are given with two integers values base and power respectively. We need to print the value representing the base raise to its power. We will design the program using recursion and also discuss the approach using iteration as well.

Example :

  • Input : 5 3
  • Output : 125
  • Explanation : 53 = 125
Power of a Number using Recursion in C++

Method 1 (Using Recursion):

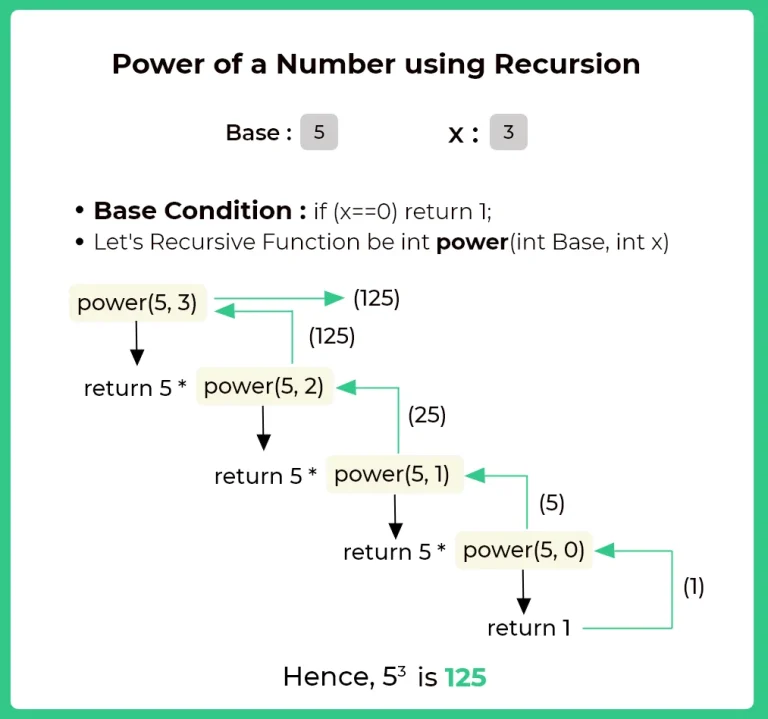
  • Create a recursive function say power(int base, int x)
  • Base condition : if(x==0) return 1.
  • Otherwise, return (base* power(base, x-1))

 

Time and Space Complexity :

  • Time Complexity : O(x), x denotes the power.
  • Space Complexity : O(1)
Power of a number

Code to find Power of a Number using Recursion in C++

Run
  #include<bits/stdc++.h>
  using namespace std;

  //Recursive Function
  int power(int base, int x){

  if(x==0) //Base Condition
    return 1;

  return (base*power(base, x-1));
 }
//Driver Code
  int main(){
  int base = 5, x = 3;
  cout<<"Required Power is "<<power(base, x);
}
Output 
Required Power is 125
 
 

Smallest element in an array

Prime Number

Largest element in an array

Method 2 (Using Loop):

  • Create a function say power(int base, int x), that will return the integer value denoting the basex.
  • Create a variable say result = 1, that hold the basex.
  • Run a while loop that will terminate when x becomes 0.
  • Inside the loop set result = result * base.
  • After complete iteration return result.

 

Time and Space Complexity :

  • Time Complexity : O(x), x denotes the power.
  • Space Complexity : O(1)

Code to find Power of a Number using loop in C++

Run 
  #include<bits/stdc++.h>
  using namespace std;

 int power(int base, int x){

  int result=1;
  while(x--){
  result *= base;
 }

 return result;
}

  //Driver Code
  int main(){
  int base = 5, x = 3;
  cout<<"Required Power is "<<power(base, x);
}
Output 
Required Power is 125

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime
While loop in C

One comment on “Power of a Number using Recursion in C++”


  • Niraj

    #include
    using namespace std;

    // Iterative power naive
    int powerOf_naiveIterative(int n, int p){
    int res = 1;
    for(int i=1;i0){
    if(p%2==1){
    res = res*n;
    }
    n = n*n;
    p = p/2;
    }
    return res;
    }

    // recursive power naive
    int recursivePower_naive(int n, int p){
    if(p==1) return n;
    return n*recursivePower_naive(n,p-1);
    }

    // recursive power effecient
    int recursivePower(int n,int p){
    if(p==1) return n;
    int temp = recursivePower(n, p/2);
    temp = temp*temp;
    if(p%2==0) return temp;
    else return temp*n;
    }

    int main(){
    int t;
    cin >> t;
    while(t–){
    int n, p;
    cin >> n >> p;
    cout << recursivePower(n,p) << endl;
    }
    }