Optimal Substructure Property

February 4, 2022

Optimal Substructure property

The Optimal Substructure property is one of the properties of the dynamic programming problems. This is an article on this Property of DP Paradigm and how to find them in a DP problem and implement them through code or enhanced recursion.

Optimal Substructure property | PrepInsta

What is Optimal Substructure property?

Optimal Substructure property is a property of the dynamic programming problem. Having this property means the problem can be solved by the solutions of the subproblems of it. That means, suppose this is a linear problem, and for getting the answer at index n, if we need to find the answer at index n-1, we will say the problem has this Property.

Example

Let us discuss the coding problem. We all know about the problem of Length of Longest Common Subsequence. This goes like, let us say there are two strings, and we have to find what is the length of the longest common subsequence possible made of the characters that are present in both of the strings in the same order.

So let us say, the words are “PREPINSTA” and “ENCODING”. So word1 is with length 9 and word2 is length 8. When we ask the Length of Longest common subsequence of word1 and word2, we actually mean to find the length of that of word1 till that’s last index and word2 till that’s last index.

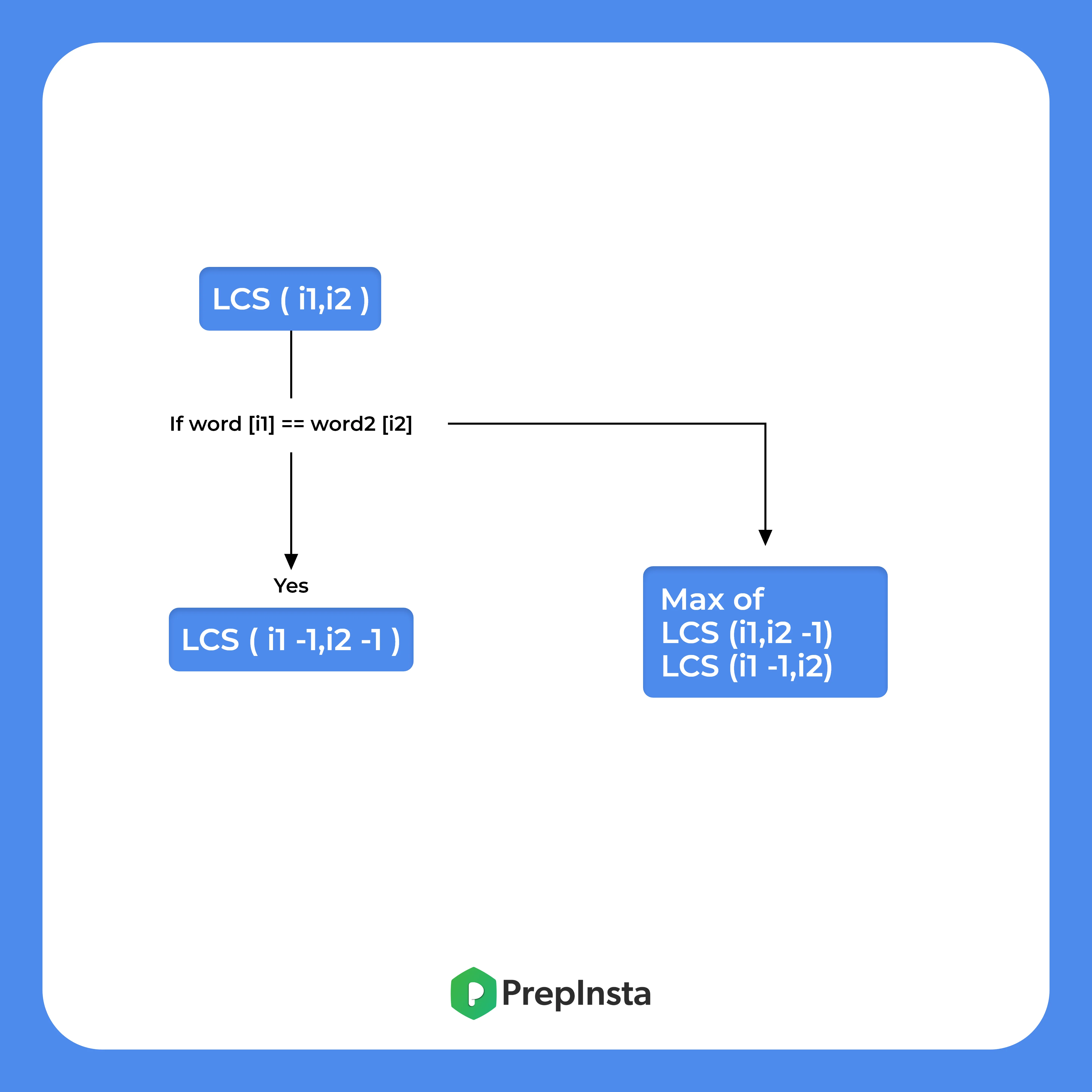
So we can write a function LCS with arguments string word1, string word2, int Index1, int Index2, and we will call the code from the last index of both words. The logic will go like,

If word1 [Index1] and word2 [Index2] are same, then return 1+ LCS(word1, word2, Index1-1,Index2).
Else return the maximum of LCS (word1, word2, Index1-1,Index2-1) and LCS (word1, word2, Index1,Index2-1)
And the base condition will be if Index1 or Index2 is less than 0.

So for two different conditions we have two different Optimal substructure properties visible and that will bring the right answer for the problem, no matter how lengthy or different the words be. This is the use of the OSP, and below we implement the algorithm in coding.

C++

Python

C++

#include <iostream>
using namespace std;

int LCS(string word1, string word2, int Index1, int Index2)
{
    if(Index1 <0 || Index2 <0) return 0;
    if(word1[Index1]==word2[Index2]) return 1+ LCS(word1,word2,Index1-1,Index2-1);
    
    return max(LCS(word1,word2,Index1,Index2-1),LCS(word1,word2,Index1-1,Index2));
}

int main()
{
    string word1 = "PREPINSTA", word2 = "ENCODING";
    cout<<LCS(word1,word2,word1.length()-1,word2.length()-1);
}