Minimum Jumps to Reach End

October 18, 2024

Minimum Jumps to Reach End

In the minimum jumps to reach the end problem as the name suggests we have to find the minimum jumps required to reach the destination position from starting position. In this article, we provide a C++ solution with an explanation.

Minimum Jumps to Reach End Problem Description

Minimum Jumps to Reach End Problem Description

Given an array of n integers. Each integer corresponds to the maximum jump length that can be made from its position in forward direction. We are required to find the minimum no. of jumps required to reach the end position (ie nth position).

Input:

  • First-line contains integer n – the final position.
  • The next line contains n integers – the maximum jump possible from the current position.

Output:

  • Single Integer – the required number of jumps to reach nth position.

Solution Explanation

Hint – This problem has a similar solution as the longest increasing subsequence (LIS) problem.

Algorithm –

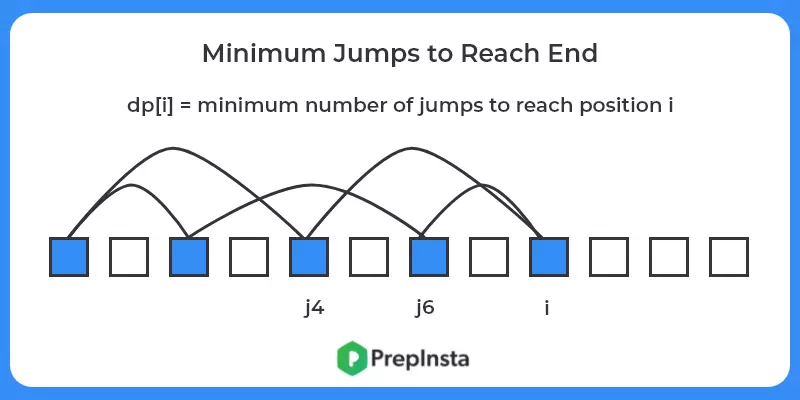
  • Create a dp array of size n where dp[i] = minimum number of jumps required to reach i from starting position.
  • To compute dp[i], we will check all positions j, such that j < i and i is reachable from j.
  • Using nested loops we can compute dp[i] and further use recalculated values to find solution for new values.
  • Return dp[n-1] (0 based indexing) as answer. Refer to the code below for more details.

Time Complexity – O(n^2) As we are using nested loops.

Space Complexity – O(n) As we created dp array of size n.

Minimum Jumps to Reach End Explanation

Code

Run 
#include < bits/stdc++.h>

using namespace std;

int minJumps(int arr[], int n)

{

    int dp[n];

    dp[0] = 0; // As we are already at this position

    for (int i = 1; i < n; i++)

        dp[i] = INT_MAX; // Marking positions unreachable

    for (int i = 1; i < n; i++)

    {

        for (int j = 0; j < i; j++)

        {

            //i is reachable from j

            if (j + arr[j] >= i)

            {

                dp[i] = min(dp[i], 1 + dp[j]);

            }

        }

    }

    return dp[n - 1];

}

int main()

{

    int n = 5;

    int arr[5] = {1, 2, 3, 4, 5};

    int ans = minJumps(arr, 5);

    cout << ans << endl;

    return 0;

}

Output

3

Explanation

1 -> 2 -> 4 -> 5