Longest Increasing Subsequence

November 6, 2021

Longest Increasing Subsequence

In the Longest Increasing Subsequence problem, we are asked to find the length of the longest increasing subsequence. It is a very famous problem that is asked in many coding rounds and interviews. Here we provide a c++ solution with an explanation of the problem.

Longest Increasing Subsequence Problem Desciption

We are given an array of n integers. What is the length of longest increasing subsequence.

Input:

First line contains integer n – The size of array.
Second line contains n integers.

Output:

The largest possible length.

Longest Increasing Subsequence Problem Solution Explanation

Solution (Top Down):

To build a top down solution we must follow the following steps –

Break Down the Problem – Let’s suppose we create a function that outputs the length of longest increasing subsequence at index i.

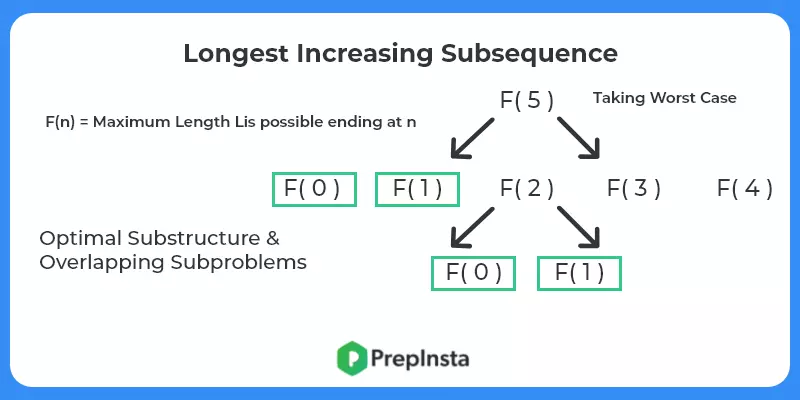
F(i) = Length of Longest Increasing Subsequence ending at i.What can be our transitions?

F(i) = 1 + F(j) where j belongs to [0,i-1] such that arr[j] <= arr[i]

Find the base case – Base case is int solution of smallest known problem. In this problem we know that F(0) = 1 (ie we only have one element in array and no left before it).
Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 10005;
int memo[N];
int lis(int arr[], int idx)
{
    if (idx == 0)
        return 1;
    if (memo[idx] != –1)
        return memo[idx];

    int ans = 1;

    for (int i = idx – 1; i >= 0; i–)
    {
        if (arr[i] <= arr[idx])
            ans = max(ans, 1 + lis(arr, i));
    }

    return memo[idx] = ans;
}
/*
    Auxiliary function getting lis ending at every index i
*/
int auxF(int arr[], int n)
{
    int ans = 0;
    for (int i = n – 1; i >= 0; i–)
    {
        ans = max(ans, lis(arr, i));
    }
    return ans;
}
int main()
{
    memset(memo, –1, sizeof memo);
    int n = 6;
    int arr[n] = {1, 3, 2, 5, 8, 2};
    cout <<“Lis is “ << auxF(arr, n) << endl;
    return 0;
}

Output

Lis is 4

Bottom up Solution

Here we create a dp array of length n. We iterate over dp array from 0 to n-1. For every index i we check all possible indices j, whether current index i can extend j.

Code

#include <bits/stdc++.h>
using namespace std;
int lis(int arr[], int n)
{
    int dp[n];
    int ans = 0;
    for (int i = 0; i < n; i++)
    {
        dp[i] = 1;
        for (int j = 0; j < i; j++)
        {
            if (arr[j] <= arr[i])
                dp[i] = max(dp[i], 1 + dp[j]);
        }

        ans = max(ans, dp[i]);
    }
    return ans;
}

int main()
{
    int n = 6;
    int arr[n] = {1, 3, 2, 5, 8, 2};
    cout << “Lis is” << lis(arr, n) << endl;
    return 0;
}

Output

Lis is 4