Cutting a Rod
Cutting a Rod
In the Cutting a Rod problem we are given a large rod. We have to cut the rod into smaller pieces to maximize the price. In this article, we provide C++ code with an explanation of the problem.

Cutting a Rod Problem Description
In this problem we are given a rod of size n. We are also given the selling price of smaller rods each of size 1 to n. We have to make multiple cuts on the larger rod in order to maximize the selling price.
Input:
- First line contains integer n – The size of rod.
- Second line contains n integers – Selling prices of rods of length 1 to n.
Output:
- The maximum price achievable.
Cutting a Rod Solution
Memoization or Top Down Solution
To build a top-down solution we must follow the following steps –
- Break Down the Problem – In this step, we try to break down the problem into smaller problems and assume recursion will solve the smaller problems.
F(N) = Max price achievable for a rod of length N.
F(N) = max( F(N-i)+cost[i]) { i belongs to 1 to N}
- Find the base case – The base case is the smallest known solution. Here it is when the length is 0 we return 0 cost.
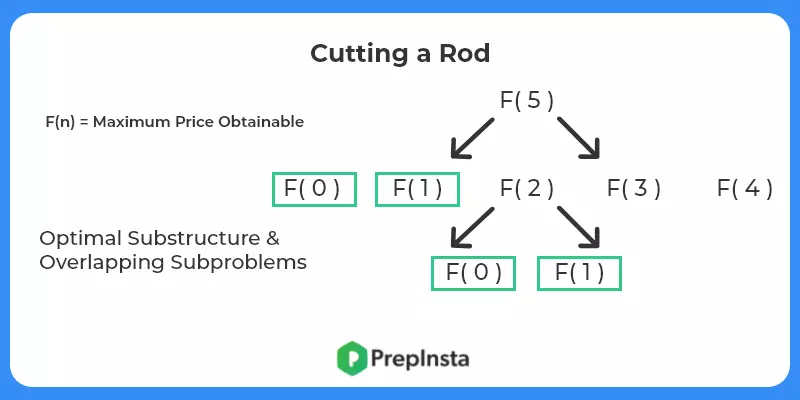
- Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 10005;
int memo[N];
int f(int cost[], int n)
{
if (n <= 0)
return 0;
if (memo[n] != –1)
return memo[n];
int ans = INT_MIN;
for (int cut = 1; cut <= n; cut++)
{
int cur = cost[cut – 1] + f(cost, n – cut);
ans = max(ans, cur);
}
return memo[n] = ans;
}
int main()
{
memset(memo, –1, sizeof memo);
int n = 5;
int arr[n] = {1, 2, 3, 2, 1};
cout << “Maximum Cost is “ << f(arr, n) << endl;
return 0;
}
Output
Maximum Cost is 5
Bottom up Solution
Here we create a dp array of length n+1. We find the maximum price for each length starting from length = 1 to length = n.
Code
#include <bits/stdc++.h>
using namespace std;
int f(int cost[], int n)
{
int dp[n + 1];
dp[0] = 0;
for (int length = 1; length <= n; length++)
{
dp[length] = INT_MIN;
for (int cut = 1; cut <= length; cut++)
{
dp[length] = max(dp[length], cost[cut – 1] + dp[length – cut]);
}
}
return dp[n];
}
int main()
{
int n = 5;
int arr[n] = {1, 2, 3, 2, 1};
cout << “Maximum Cost is “ << f(arr, n) << endl;
return 0;
}
Output
Maximum Cost is 5



Login/Signup to comment