Count ways to reach the n’th stair

December 7, 2021

Count ways to reach the n’th stair

In count ways to reach the n’th stair problem we have to find number of ways in which we can reach the nth stair. The solution of this problem is similar to dynamic programming solution used to find nth Fibonacci number. In this article we provide a C++ solution with an explanation.

Count ways to reach the n’th stair Problem Description

Count ways to reach the n’th stair Problem Description

Given a stair with n steps. At a time you can take a step of size 1 or 2. Find the number of ways you can reach the top.

Input:

  • A single line containing integer n.

Output:

  • Single integer the required number of ways.

Count ways to reach the n’th stair Problem Solution

Hint – This problem has similar solution used to find nth Fibonacci number using dynamic programming.

Solution (Top Down):

To build a top down solution we must follow the following steps –

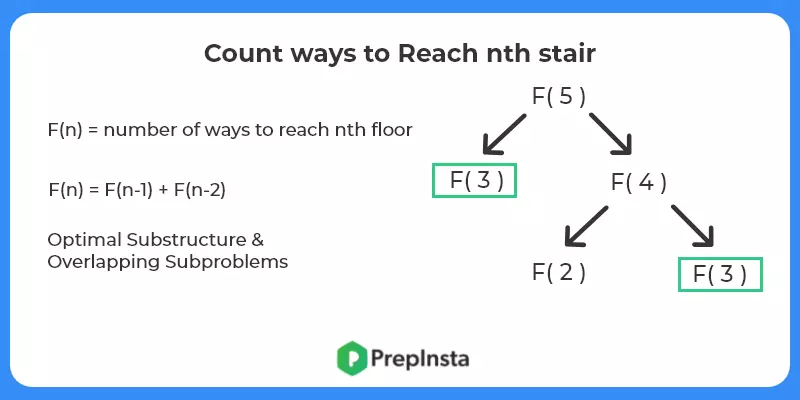
  • Break Down the Problem –Let’s suppose we have a function F(x) that outputs number of ways to to reach the xth stair using 1 or 2 steps. Then – 

F(x) = F(x-1) + F(x-2)

ie Reach xth position from x-1 by taking step of size 1 + Reach xth position from x-2 by taking step of size 2.

  • Find the base case – Base case is the solution of smallest known problem. In this problem we know that F(1) = 1 (1 stair so only choice is 1 step) & F(2) = 2 { Take 1, 1 or 2 steps }.
  • Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. {Same as Fibonacci numbers}.

Time & Space Complexity – O(n)

Bottom up Solution

Here we create a dp array of length n+1. And use similar transition as above.

Time & Space Complexity – O(n)

Space Optimized Solution

Since the recurrence relation is similar to Fibonacci number problem we can write a space optimized solution.

Time complexity – O(n)

Space Complexity – O(1)

Count ways to reach the n’th stair Problem BreakDown

Code

#include <bits/stdc++.h>
using namespace std;
// top down solution
int memo[1005];
int f(int n)
{
    if (n <= 2)
        return n;
    if (memo[n] != –1)
        return memo[n];
                    // Take 1 step or 2
    return memo[n] = f(n – 1) + f(n – 2);
}
// Bottom Up
int bottomUp(int n)
{
    int dp[n + 1];
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i++)
        dp[i] = dp[i – 1] + dp[i – 2];
    return dp[n];
}
// Space optimized
int spaceOptimized(int n)
{
    if (n <= 2)
        return n;
    int cur = 2, prev = 1;
    for (int i = 3; i <= n; i++)
    {
        int next = cur + prev;
        prev = cur;
        cur = next;
    }
    return cur;
}
int main()
{
    memset(memo, –1, sizeof memo);
    cout << f(5) << endl;
    cout << bottomUp(5) << endl;
    cout << spaceOptimized(5) << endl;
    return 0;
}

Output

8
8
8