Coin Change Problem

November 6, 2021

Coin Change Problem

In the coin change problem, we have to count the number of ways of making change given an infinite supply of some coins. Here is a C++ implementation explaining the bottom-up and top-down solutions.

Coin Change Problem Description

We are given a value N ( rupees ). And we are given infinite value of M coins. What are the total number of ways we can make change using m coins. The order of coins doesn’t matter.

Input:

First line containing integer denoting total rupees for which we have to make change.
Second line contains integer m denoting number of coins.
Third line contains m integers denoting the denomination of each coin.

Output:

Number of ways to make change.

Coin Change Problem Solution Explanation

Solution (Top Down):

To build a top down solution we must follow the following steps –

Break Down the Problem –Since the order of a coin does not matter, the idea is to pick a coin and keep using it till you can. If at any point we decided to not pick the coin then we never pick this coin again. The recurrence relation is –

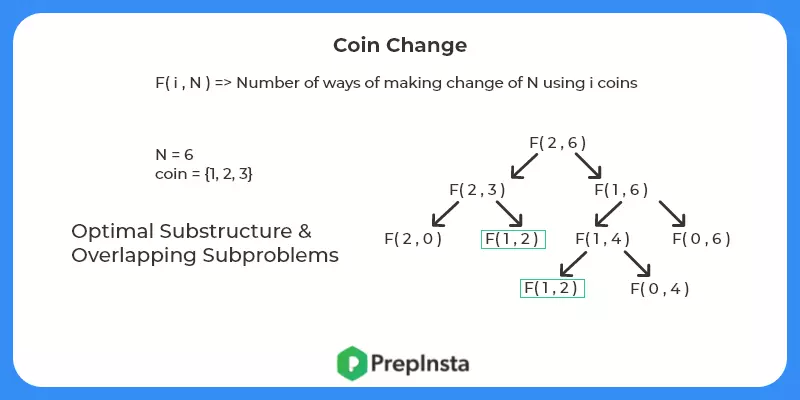
F(i,N) = Number of ways to make change of N using first i coins.

F(i,N) = F(i,N-coin[i]) + F(i-1,N) { ie using ith coin or not using ith coin}

Find the base case – We know if N is zero then we have 1 way which is 0 coins . If N becomes negative then there are zero ways. And the third base case is when we are left with zero coins but a positive value of N.
Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.

C++ Code:

#include <bits/stdc++.h>
using namespace std;
int dp[1005][1005];
// cur means current coin index
// changeLeft means amount we want to change
int f(int coin[], int cur, int changeLeft)
{
    // If no change left
    if (changeLeft == 0)
        return 1;
    // If change left is negative
    if (changeLeft < 0)
        return 0;

    // If no coin is left and we have positive value of money left.
    if (cur < 0 && changeLeft >= 1)
        return 0;

    if (dp[cur][changeLeft] != –1)
        return dp[cur][changeLeft];

    return dp[cur][changeLeft] = f(coin, cur – 1, changeLeft) + f(coin, cur, changeLeft – coin[cur]);
}
int main()
{
    memset(dp, –1, sizeof dp);
    int n;
    cin >> n;
    int m;
    cin >> m;
    int coin[m];
    for (int i = 0; i < m; i++)
    {
        cin >> coin[i];
    }

    cout << “Number of ways “ << f(coin, m – 1, n) << endl;
    return 0;
}

Output:

6
3
1 2 3
Number of ways 7

Solution (Bottom Up)

For bottom up solution the idea is similar as above. We create a dp table where,

dp[i] = Number of Ways to make change for i rupees.

Now we just pick one coin at a time and fill the dp table.

C++ Code:

#include <bits/stdc++.h>
using namespace std;
int f(int coin[], int n, int m)
{
    int dp[n + 1] = {0};
    dp[0] = 1;
    for (int i = 0; i < m; i++)
    {
        // Pick and use ith coin
        for (int j = coin[i] ; j <= n; j++)
        {
            dp[j] += dp[j–coin[i]];
        }
    }
    return dp[n];
}
int main()
{
    int n;
    cin >> n;
    int m;
    cin >> m;
    int coin[m];
    for (int i = 0; i < m; i++)
    {
        cin >> coin[i];
    }

    cout << “Number of ways “ << f(coin, n, m) << endl;
    return 0;
}

Output:

6
3
1 2 3
Number of ways 7