Insertion in a Binary Tree (Level Order) in C

March 20, 2025

Insertion in a binary tree

 

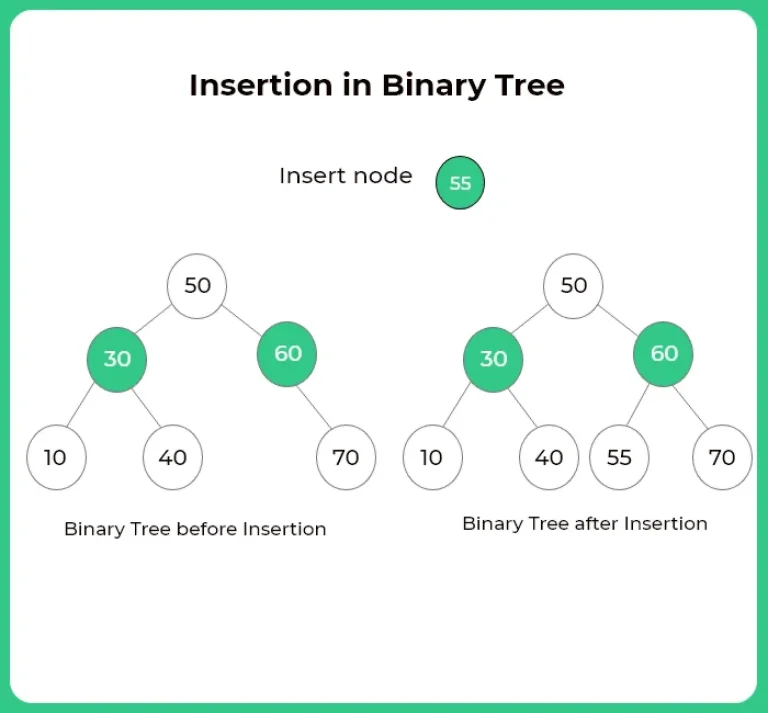
Given a tree and a key, add a node in the first available node in the tree. After adding the node, print the level order traversal. In this article, Queue data structure is used to add a node.

Insertion in tree in C

Insertion in a Binary Tree In C

Algorithm :

  • Create a queue q.
  • If root is NULL, add node and return.
  • Else continue until q is not empty.
  • If a child does not exists, add the node there.
  • Otherwise add the node to the leftmost node.
insertion in binary tree

AVL Trees

AVL Tree Insertion

AVL Tree Deletion

Find size of the Binary tree

Find height of the Binary Tree

C code for insertion a node in binary tree

Run 
#include<stdio.h>
#include<stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node
{
  int data;
  struct Node *left;
  struct Node *right;
};
struct Node *newNode (int data)
{
  struct Node *Node = (struct Node *) malloc (sizeof (struct Node));
  Node->data = data;
  Node->left = NULL;
  Node->right = NULL;

  return (Node);
};

void printCurrentLevel (struct Node *root, int level);
int height (struct Node *node);

int height (struct Node *node)
{
  if (node == NULL)
    return 0;
  else
    {
/* compute the height of each subtree */
      int lheight = height (node->left);
      int rheight = height (node->right);

/* use the larger one */
      if (lheight > rheight)
	return (lheight + 1);
      else
	return (rheight + 1);
    }
}

void printLevelOrder (struct Node *root)
{
  int h = height (root);
  int i;
  for (i = 1; i <= h; i++)
    printCurrentLevel (root, i);
}				/* Print nodes at a current level */

void printCurrentLevel (struct Node *root, int level)
{
  if (root == NULL)
    return;
  if (level == 1)
    printf ("%d ", root->data);
  else if (level > 1)
    {
      printCurrentLevel (root->left, level - 1);
      printCurrentLevel (root->right, level - 1);
    }
}

struct Node *insert (struct Node *root, int val)
{

  if (root == NULL)
    return newNode (val);

  if (root->data < val)
    root->right = insert (root->right, val);

  else if (root->data > val)
    root->left = insert (root->left, val);

  return root;
}

// Driver code
int main ()
{
  struct Node *root = newNode (10);
  root->left = newNode (11);
  root->left->left = newNode (7);
  root->right = newNode (9);
  root->right->left = newNode (15);
  root->right->right = newNode (8);

  printf ("Level order traversal before insertion: ");
  printLevelOrder (root);
  printf ("\n");

  int key = 12;
  root = insert (root, key);

  printf ("Level order traversal after insertion: ");
  printLevelOrder (root);
  printf ("\n");

  return 0;
}

Output :


Level order traversal before insertion : 10 11 9 7 15 8

Level order traversal after insertion : 10 11 9 7 15 8 12