Count ways to reach the n’th stair
Count ways to reach the n’th stair
In count ways to reach the n’th stair problem we have to find number of ways in which we can reach the nth stair. The solution of this problem is similar to dynamic programming solution used to find nth Fibonacci number. In this article we provide a C++ solution with an explanation.

Count ways to reach the n’th stair Problem Description
Given a stair with n steps. At a time you can take a step of size 1 or 2. Find the number of ways you can reach the top.
Input:
- A single line containing integer n.
Output:
- Single integer the required number of ways.
Count ways to reach the n’th stair Problem Solution
Hint – This problem has similar solution used to find nth Fibonacci number using dynamic programming.
Solution (Top Down):
To build a top down solution we must follow the following steps –
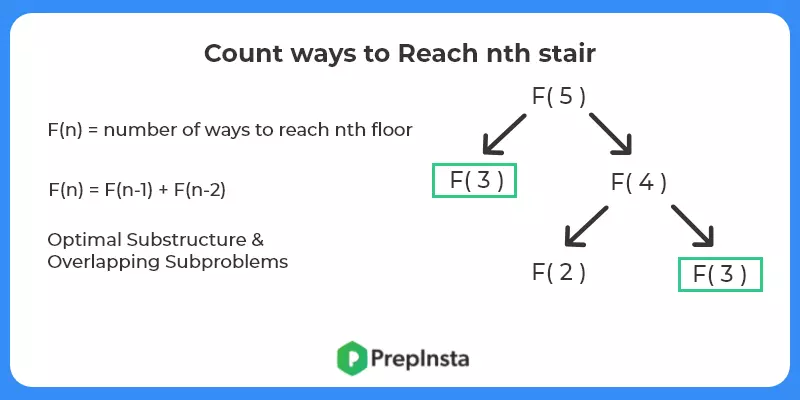
- Break Down the Problem –Let’s suppose we have a function F(x) that outputs number of ways to to reach the xth stair using 1 or 2 steps. Then –
F(x) = F(x-1) + F(x-2)
ie Reach xth position from x-1 by taking step of size 1 + Reach xth position from x-2 by taking step of size 2.
- Find the base case – Base case is the solution of smallest known problem. In this problem we know that F(1) = 1 (1 stair so only choice is 1 step) & F(2) = 2 { Take 1, 1 or 2 steps }.
- Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. {Same as Fibonacci numbers}.
Time & Space Complexity – O(n)
Bottom up Solution
Here we create a dp array of length n+1. And use similar transition as above.
Time & Space Complexity – O(n)
Space Optimized Solution
Since the recurrence relation is similar to Fibonacci number problem we can write a space optimized solution.
Time complexity – O(n)
Space Complexity – O(1)
Code
Output
8
8
8



Login/Signup to comment