Tiling Problem

December 7, 2021

Tiling Problem

In the tiling problem, we have to find the number of ways to fill a board. The problem has a similar solution as the Fibonacci number using dynamic programming. In this article, we have a C++ solution with an explanation.

Tiling Problem Description

Tiling Problem Description

We are given a land of 2*n. We are given infinite supply of 2*1 tiles. We can place these tiles either horizontally or vertically. Find the number of ways to cover the land.

Input:

  • First line contains integer n – The width of land.

Output:

  • Required number of ways

Tiling Problem Solution Explanation

Hint – This problem has similar solution used to find nth Fibonacci number using dynamic programming.

Solution (Top Down):

To build a top down solution we must follow the following steps –

  • Break Down the Problem –Let’s suppose we have a function F(x) that outputs number of ways to fill a land of 2*x dimension. Then – 

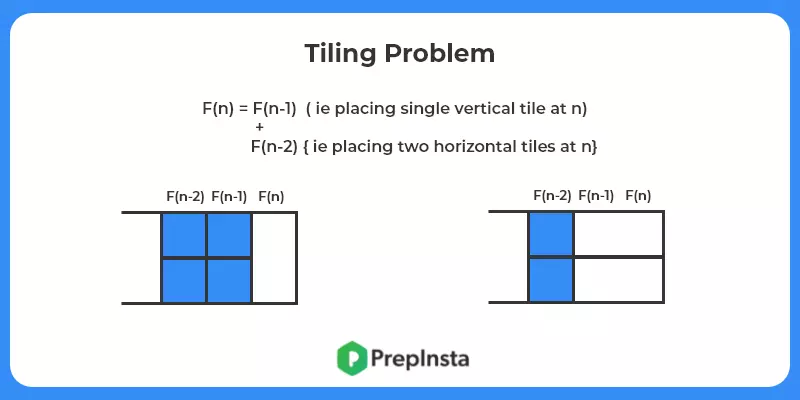
F(x) = F(x-1) + F(x-2)

ie Place a vertical tile at nth Position + Place vertical tile at (n-1)th position.

  • Find the base case – Base case is the solution of smallest known problem. In this problem we know that F(1) = 1 (We can have only 1 file in vertical orientation) & F(2) = 2 { 2 tiles in vertical orientation or 2 tiles in horizontal orientation}.
  • Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. {Same as Fibonacci numbers}.

Time & Space Complexity – O(n)

Tiling Problem BreakDown

Code

#include<bits/stdc++.h>
using namespace std;
int dp[1005];
int f(int n)
{
    if(n<=2)
        return n;
    if(dp[n]!=-1)
        return dp[n];
    return dp[n] = f(n–1) + f(n–2);
}
int main()
{
    memset(dp,-1,sizeof dp);
    int n;
    cin>>n;
    cout<<f(n)<<endl;
}

Output

3
3

Bottom up Solution

Here we create a dp array of length n+1. And use similar transition as above.

Time & Space Complexity – O(n)

Code

#include <bits/stdc++.h>
using namespace std;
int dp[1005];
int f(int n)
{
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= n; i++)
        dp[i] = dp[i – 1] + dp[i – 2];
    return dp[n];
}
int main()
{
    int n;
    cin >> n;
    cout << f(n) << endl;
}

Output

3
3