Palindrome Partitioning
Palindrome Partitioning
Palindrome partitioning is a important problem which has a dynamic programming solution. It is a famous problem asked in many interviews. Here we provide C++ solution with an explanation.

Palindrome Partitioning Problem Description
Given a string, we have to determine minimum cuts we need to make such that the sub-strings obtained after cutting the original string form a palindrome.
Input
- Single line input containing input string.
Output
- Single integer the required number of cuts.
Example
Input 1
- aabbcc
Output 1
- 2
Explanation 1
- Sub strings are aa, bb, cc.
Palindrome Partitioning Problem Solution
Memoization or Top Down Solution
To build a top down solution we must follow the following steps –
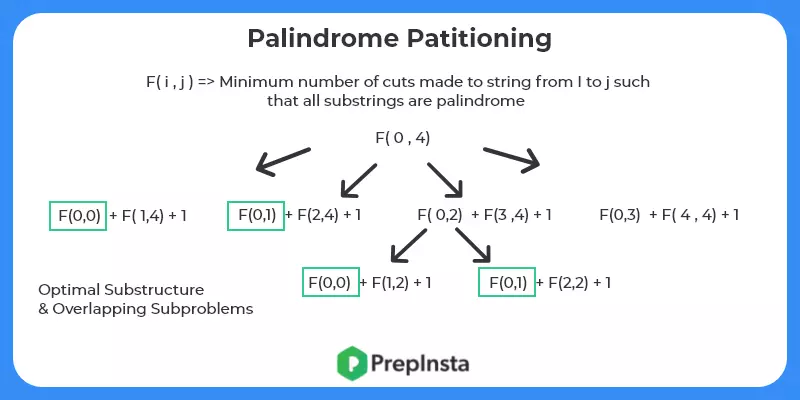
- Break Down the Problem – In this step we try to break down the problem into smaller problems and assume recursion will solve the smaller problems.F(i,j) = Min no. of cuts made in the string (from i to j) such that all sub strings all palindromes. To get the value of F(i,j) we need to divide string from i to j into two parts and recursively find minimum cuts for them.
- Find the base case – Base case is easy in this problem. One base case is if we have a string of length 1 (ie i==j) then we simple return 0 as it is a palindrome of length 1. If we reach an invalid sequence (i>j) , then also we simple return 0. The other base case is if the current string is itself a palindrome, then no need to cut it.
- Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
Bottom Up Solution
In this approach we solve smaller problems first instead of shoving for bigger problems.We create a table cuts[n][n] (n = string length).
Using similar transitions as above we can get our answer.
Code
#include <bits/stdc++.h>
using namespace std;
int memo[505][505];
// function to check whether a string is palindrome or not
bool checkPalindrome(string &s, int i, int j)
{
while (i <= j)
{
if (s[i] != s[j])
return false;
i++;
j–;
}
return true;
}
// Top Down
int cuts(string &str, int i, int j)
{
if (i >= j)
return 0;
if (checkPalindrome(str, i, j))
return 0;
if (memo[i][j] != –1)
return memo[i][j];
int ans = INT_MAX;
// Making cuts
for (int k = i; k < j; k++)
{
int cur = 1 + cuts(str, i, k) + cuts(str, k + 1, j);
ans = min(ans, cur);
}
return memo[i][j] = ans;
}
int bottomUp(string s)
{
int n = s.length();
int cuts[n][n]; // Minimum cuts from i to j
bool dpPalindrome[n][n]; // Used to check is substring i to j is palindrome or not
for (int i = 0; i < n; i++)
{
dpPalindrome[i][i] = true;
cuts[i][i] = 0;
}
for (int length = 2; length <= n; length++)
{
for (int i = 0; i < n – length + 1; i++)
{
int j = i + length – 1;
if (length == 2)
dpPalindrome[i][j] = (s[i] == s[j]);
else
dpPalindrome[i][j] = (s[i] == s[j]) && dpPalindrome[i + 1][j – 1];
if (dpPalindrome[i][j] == true)
cuts[i][j] = 0;
else
{
cuts[i][j] = INT_MAX;
for (int k = i; k < j; k++)
{
cuts[i][j] = min(cuts[i][j], cuts[i][k] + cuts[k + 1][j] + 1);
}
}
}
}
return cuts[0][n – 1];
}
int main()
{
memset(memo, –1, sizeof memo);
string s;
cin >> s;
cout << cuts(s, 0, s.length() – 1) << endl;
cout << bottomUp(s) << endl;
return 0;
}
Output
aabbcc
2
2




Login/Signup to comment