0-1 Knapsack Problem
0-1 Knapsack Problem
In 0-1 Knapsack Problem, we are asked to fill a knapsack according to some constraints. This problem and its variations are one of the most asked interview problems. In this article, we explain the solution to the problem with c++ implementation.

0-1 Knapsack Problem Description
We are given a knapsack which has a capacity of C ie the knapsack can carry items of total weight less than or equal to C. Each item has a weight and value/price associated to it. We are given n items, determine the maximum value of the knapsack we can obtain by filling some subset of the n items.
Input:
- First line contains an integer C, the capacity of the knapsack.
- Second line contains a single integer n, the number of items.
- Third line contains n integers, the value of n items. Value is ith item is ith integer.
- Fourth line contains n integers, the weight of n items. Weight of ith item is ith integer.
Output:
- Single Integer, the maximum value obtainable.
0-1 Knapsack Problem Solution
Memoization or Top Down Solution
To build a top down solution we must follow the following steps –
- Break Down the Problem – In this step we try to break down the problem into smaller problems and assume recursion will solve the smaller problems.
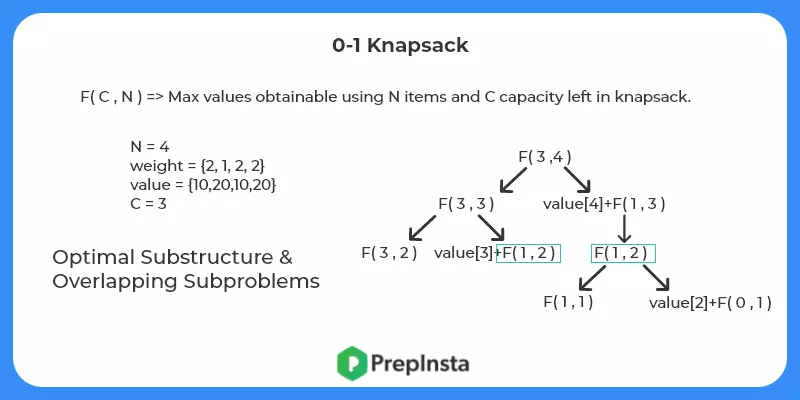
F(C,N) = Maximum value of filling C capacity knapsack with N items.
This can be broken down into two cases – when we put the nth item in the knapsack or we discard the nth item.
Thus,
F(C,N) = F(C,N-1) { if (weight[N] > C We can’t include this item))}
F(C,N) = max(F(C,N-1) , value[n] + F(C-weight[N],N-1)) {We don’t include or we include}
- Find the base case- Now we have to find the base case. It is easy as we can’t include items if C = 0 ie capacity of knapsack is zero or N = 0 ie we don’t have items left to process.
- Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
C++ Code:
Output:
40
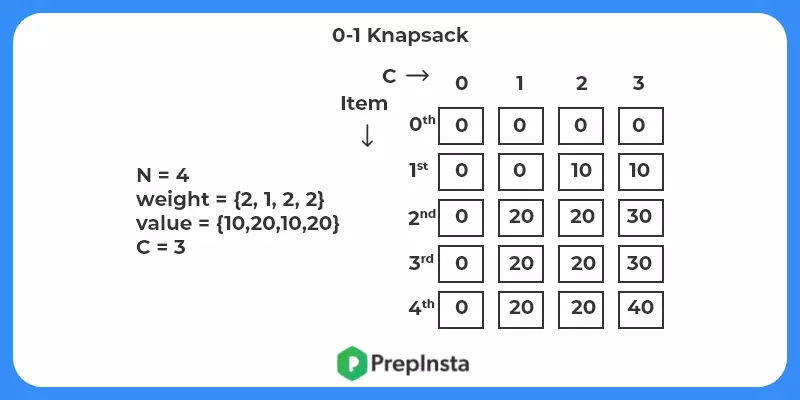
Bottom Up Solution
In this approach we solve smaller problems first instead of shoving for bigger problems. We create a dp table of size N*W where
dp[i][w] = maximum value of filling w capacity knapsack with i items.
Using similar transitions as above we can get our answer.
C++ Code:
Output:
Ans -> 40



Login/Signup to comment