Binary Search in C++

May 24, 2022

What is binary search in C++?

Binary search is another searching algorithm in C++. It is also known as half interval search algorithm. It is an efficient and fast searching algorithm.

  • The only condition required is that the elements in the list must be in sorted order.
  • It works by repeatedly dividing in half the portion of the list that could contain the item, until you’ve narrowed down the possible locations to just one.
binary
Time Complexity (Best) Ω(1)
Time Complexity (Avg) Θ(log n)
Time Complexity (Worst) O(log n)
Space Complexity O(1)

Working of binary search in C++

  1. It works when the list is in sorted order either ascending or descending.
  2. Calculate the mid using formula
  3. If the element is in the mid then stop searching.
  4. Else if the search item is greater than mid. Look right half of the array
  5. Else if the search item is smaller than mid look for it in the left half of the array 
  6. We will follow steps 3, 4 and 5 until our element is found.
Binary Search in C++

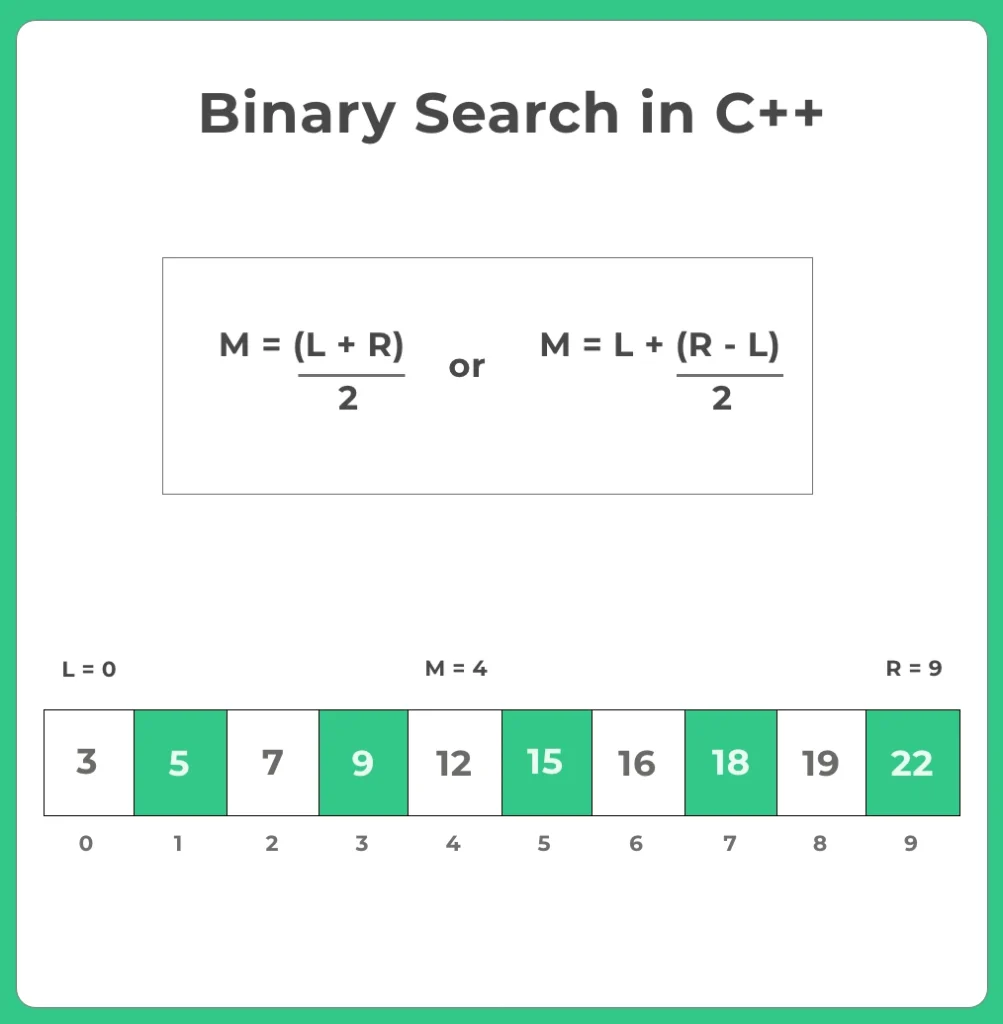
Algorithm for Binary Search in C++

  • while(left<=right)
          mid=left + (right – left)/2;
  • if(a[mid]<item)
          left=mid+1;
  • else if(a[mid]>item)
          right=mid-1;
  • If found return index+1
  • Else return -1

Methods Discussed

We will take a look at two different approaches

  • Recursive Approach
  • Iterative Approach

Binary Search in C++ (Recursive Approach)

Run 
// Binary Search implimentation in C++ (Recursive)
// Time Complexity : O(N)
// Space Complexity : O(1)
// Auxiliary Space Complexity : O(N) due to function call stack
#include<bits/stdc++.h>
using namespace std;

int binarySearch(int array[], int left, int right, int item){
    
    if (right >= left){
        
        // calculation of new mid
        int mid = left + (right - left)/2;

        // returns position where found
        if (array[mid] == item)
            return mid+1;
        
        // goes to recursive calls in left half
        if (array[mid] > item)
            return binarySearch(array, left, mid-1, item);
    
        // goes to recursive calls in right half
        else
            return binarySearch(array, mid+1, right, item);
    }
    // if element is not found we return -1
    else
       return -1;
}
int main(){
 
    int array[10] = {3, 5, 7, 9, 12, 15, 16, 18, 19, 22};
    int item = 15;
   
    int position = binarySearch(array, 0, 10, item);

    if(position == -1)
        cout<<"Not Found";
    else
        cout<<"We found the item "<< item <<" at position "<< position;
}

Output:

We found the item 15 at position 6

Binary Search in C++ (Iterative Approach)

This one is simple too let’s have a look at this approach to solve binary search.
Run 
// Binary Search implimentation in C++ (Iterative)
// Time Complexity : O(N)
// Space Complexity : O(1)
#include<bits/stdc++.h>
using namespace std;

// Returns index of item in given array, if it is present
// otherwise returns -1
int binarySearch(int arr[], int l, int r, int item)
{
    while (l <= r) {
        int mid = l + (r - l) / 2;
  
        // if item is at mid
        if (arr[mid] == item)
            return mid;
  
        // If item greater, ignore left half, consider only right half
        if (arr[mid] < item)
            l = mid + 1;
  
        // If item is smaller, ignore right half, consider only left half
        else
            r = mid - 1;
    }
  
    // if we are able to reach here
    // means item wasn't present
    return -1;
}
  
int main()
{
    // array needs to be sorted to impliment binary search
    int arr[] = {3, 5, 7, 9, 12, 15, 16, 18, 19, 22};
    int n = sizeof(arr) / sizeof(arr[0]);
    int item = 7;
    
    int position = binarySearch(arr, 0, n - 1, item);
    
    if(position == -1)
        cout << item << " Not Found";
    else
        cout << item << " Found at index " << position;
        
    return 0;
}

Output

7 Found at index 2

Advantages 

Binary search has the following advantages:-

  • Works faster than linear search.
  • It is a simple algorithm.
  • Has O(log N) time complexity

Disadvantages

  • The array needs to be in sorted order for a binary search to work

Our example uses an array sorted in ascending order, if the array was sorted in descending order we can make a few minor changes in the program and make it work for descending order too

You can also study binary search in C and Java

Binary Search in C++ Meme 1

Time Complexity
For Binary Search

Best

O(1)

Average

O(log n)

Worst

O(log n)

Space Complexity

O(1)

Average Comparisions

Log(N+1)