Recursion in C

March 30, 2022

Recursion in C

Here, on this page, we will discuss recursion in C programming language. When the function will call itself then that call is known as a recursive call and the function is known as a recursive function. Recursion involves several recursive calls.

All problems that are solved using recursion can also be solved using iterations

Recursion is made for solving problems that can be broken down into smaller, repetitive problems.

Recursion in C

Why Recursion?

  • Recursion involves calling the same function again, and hence, has a very small length of code.
  • It is especially good for working on things that have many possible branches and are too complex for an iterative approach.
  • Recursion is best suited in trees and graphs problems.

Base Condition :

In a recursive function, there must be a terminating condition to stop the recursion. That terminating condition is known as the base condition.

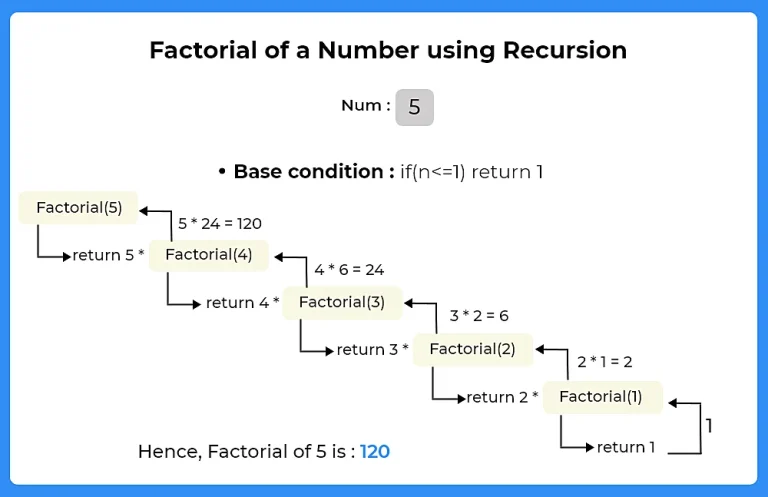
Let’s understand recursion by solving the problem of Factorial using Recursion.

Algorithm :

  • Create a function fact(int n),
  • Inside fact(), define the termination condition : if(n<=1)  return 1
  • Otherwise return n*fact(n-1) //here, we are calling function fact() again by decrement the value of n.

Time-Complexity : O(n)
Space-Complexity : O(1)

Factorial using recursion

Code to understand recursion in C

#include<stdio.h>
//Function to calculate the factorial
int fact(int n){

  if(n<=1) return 1;   //Base Condition
  else return (n*fact(n-1));   //Recurcive Call of Fact() function

}

//Driver Code
int main(){

  int n=5;
  printf("Factorial of %d is %d", n, fact(n));

}
Output :

Factorial of 5 is 120

Memory Allocation of Recursive Functions

  • Each recursive call creates a new copy of that function in the memory.
  • Once some data is returned by the function, the copy is removed from the memory.
  • Since all the variables and other stuff declared inside function get stored in the stack, therefore a separate stack is maintained at each recursive call.
  • Once the value is returned from the corresponding function, the stack gets destroyed.
  • Recursion involves so much complexity in resolving and tracking the values at each recursive call.
  • Therefore we need to maintain the stack and track the values of the variables defined in the stack.
While loop in C