C++ Program for best time to buy and sell

October 11, 2022

Best time to buy and Sell stock in C++

Here, in this page we will discuss the program to find the best time to buy and sell stock in C++  We are given with an array represents the cost of a stock on each day is given in an array, find the max profit that you can make by buying and selling in those days.

Example :

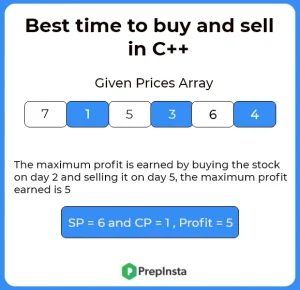
Input: Prices[ ] = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

 
Best time to buy and sell in C++

Algorithm :

  • Take the size of the array from the user and store it in variable say n.
  • Now, declare an array of size n and takes n integer value from the user and store them in array.
  • Create an array named max_sp of size equals size of price array and a variable max and initialize it as the minimum value.
  • Start from the last index in price array.
    1. If prices[i] is greater than max
      1. Update max as prices[i] and make max_sp[i] as minimum value
    2. Else if price[i] is not greater than max
      1. Update max_sp[i] = max.
  • After the pre computation, we follow the naive approach and replace the inner nested loop by using the max_sp array that we just created.
  • Print value of max.
Best time to buy and sell

Code in C++

#include <bits/stdc++.h>
using namespace std;

int maxProfit(int *prices, int n) {

  int max_sp[n];
  int maximum = INT_MIN;

  // Construct the maxSP array
  for (int i = n - 1; i >= 0; i--) {
     if (prices[i] > maximum) {
       maximum = prices[i];
       max_sp[i] = INT_MIN;
     } 
     else {
       max_sp[i] = maximum;
     }
  }

  int profit = 0;
  for (int i = 0; i < n; i++) {

    if (max_sp[i] != INT_MIN) {
      profit = max(profit, max_sp[i] - prices[i]);
   }

  }

  // Return profit
  return profit;
}

int main() {

  int n;
  cin>>n;

  int prices[n];

  for(int i=0; i<n; i++)
    cin>>prices[i];

  // Calculating the max profit
  int ans = maxProfit(prices, n);

  // Print the answer
  cout<<ans<<endl;
  return 0;
}
Input :

6

7 1 5 3 6 4

Output :

5

Given an array which consists of only 0, 1 and 2

Move all the negative elements to one side of the array

Minimum no. of Jumps to reach the end of an array 

Find Largest sum contiguous Subarray

Minimize the maximum difference between heights 

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime