Search a 2D Matrix
Program for Search in a row wise and column wise sorted matrix Problem
You are given a 2D array called matrix with m rows and n columns, and a number called target.
- Each row in the matrix is sorted in increasing order.
- The first number of each row is larger than the last number of the row before it.
Your task is to check if the target is present in the matrix. Return true if it’s found, otherwise return false. The solution should search efficiently in O(log(m * n)) time, similar to binary search in a sorted list.
Example 1
Input: matrix = [[1,2,4,8],[10,11,12,13],[14,20,30,40]], target = 10
Output: true
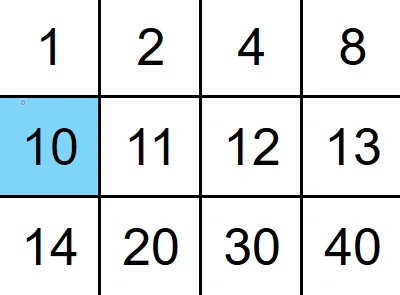
Output: true
Example 2
Input: matrix = [[1,2,4,8],[10,11,12,13],[14,20,30,40]], target = 15
Output: false
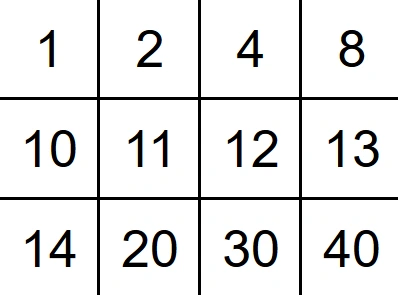
Output: false
Constraints:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -10000 <= matrix[i][j], target <= 10000
Program for Search in a row wise and column wise sorted matrix Solution
Recommendation for Time and Space Complexity – You should aim for a solution with O(log(m * n)) time and O(1) space, where m is the number of rows and n is the number of columns in the matrix.
Hints for solving problems
Hint 1 :
A brute force solution would be to do a linear search on the matrix. This would be an O(m * n) solution. Can you think of a better way? Maybe an efficient searching algorithm, as the given matrix is sorted.
Hint 2 :
We can use binary search, which is particularly effective when we visualize a row as a range of numbers, [x, y] where x is the first cell and y is the last cell of a row. Using this representation, it becomes straightforward to check if the target value falls within the range. How can you use binary search to solve the problem?
There are mainly 4 approach to solve this problem-
- Brute Force Method
- Staircase Search Method
- Binary Search Method
- Binary Search(One Pass) Method
1. Brute Force Method
Iterate through every element in the matrix and compare it with the target until a match is found.
- Time complexity: O(m*n)
- Space complexity: O(1)
where m is the number of rows and n is the number of columns of matrix.
Code
C++
Java
Python
JavaScript
C++
class Solution {
public:
bool searchMatrix(vector>& matrix, int target) {
for (int r = 0; r < matrix.size(); r++) {
for (int c = 0; c < matrix[r].size(); c++) {
if (matrix[r][c] == target) {
return true;
}
}
}
return false;
}
};
Java
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
for (int r = 0; r < matrix.length; r++) {
for (int c = 0; c < matrix[r].length; c++) {
if (matrix[r][c] == target) {
return true;
}
}
}
return false;
}
}
Python
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
for r in range(len(matrix)):
for c in range(len(matrix[0])):
if matrix[r][c] == target:
return True
return False
JavaScript
class Solution {
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
searchMatrix(matrix, target) {
for (let r = 0; r < matrix.length; r++) {
for (let c = 0; c < matrix[r].length; c++) {
if (matrix[r][c] == target) {
return true;
}
}
}
return false;
}
}
2. Staircase Search Method
Start from the top-right or bottom-left corner, move left if the target is smaller, or move down if the target is larger.
- Time complexity: O(m+n)
- Space complexity: O(1)
where m is the number of rows and n is the number of columns of matrix.
Code
C++
Java
Python
JavaScript
C++
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
int r = 0, c = n - 1;
while (r < m && c >= 0) {
if (matrix[r][c] > target) {
c--;
} else if (matrix[r][c] < target) {
r++;
} else {
return true;
}
}
return false;
}
};
Java
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length, n = matrix[0].length;
int r = 0, c = n - 1;
while (r < m && c >= 0) {
if (matrix[r][c] > target) {
c--;
} else if (matrix[r][c] < target) {
r++;
} else {
return true;
}
}
return false;
}
}
Python
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
m, n = len(matrix), len(matrix[0])
r, c = 0, n - 1
while r < m and c >= 0:
if matrix[r][c] > target:
c -= 1
elif matrix[r][c] < target:
r += 1
else:
return True
return False
JavaScript
class Solution {
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
searchMatrix(matrix, target) {
const m = matrix.length, n = matrix[0].length;
let r = 0, c = n - 1;
while (r < m && c >= 0) {
if (matrix[r][c] > target) {
c--;
} else if (matrix[r][c] < target) {
r++;
} else {
return true;
}
}
return false;
}
}
3. Binary Search Method
Treat the 2D matrix as a flattened 1D array and apply binary search by calculating mid-row and mid-column indices.
- Time complexity: O(log m + log n)
- Space complexity: O(1)
where m is the number of rows and n is the number of columns of matrix.
Code
C++
Java
Python
JavaScript
C++
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int ROWS = matrix.size();
int COLS = matrix[0].size();
int top = 0, bot = ROWS - 1;
while (top <= bot) { int row = (top + bot) / 2; if (target > matrix[row][COLS - 1]) {
top = row + 1;
} else if (target < matrix[row][0]) {
bot = row - 1;
} else {
break;
}
}
if (!(top <= bot)) {
return false;
}
int row = (top + bot) / 2;
int l = 0, r = COLS - 1;
while (l <= r) { int m = (l + r) / 2; if (target > matrix[row][m]) {
l = m + 1;
} else if (target < matrix[row][m]) {
r = m - 1;
} else {
return true;
}
}
return false;
}
};
Java
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int ROWS = matrix.length;
int COLS = matrix[0].length;
int top = 0, bot = ROWS - 1;
while (top <= bot) {
int row = (top + bot) / 2;
if (target > matrix[row][COLS - 1]) {
top = row + 1;
} else if (target < matrix[row][0]) {
bot = row - 1;
} else {
break;
}
}
if (!(top <= bot)) {
return false;
}
int row = (top + bot) / 2;
int l = 0, r = COLS - 1;
while (l <= r) {
int m = (l + r) / 2;
if (target > matrix[row][m]) {
l = m + 1;
} else if (target < matrix[row][m]) {
r = m - 1;
} else {
return true;
}
}
return false;
}
}
Python
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
ROWS, COLS = len(matrix), len(matrix[0])
top, bot = 0, ROWS - 1
while top <= bot:
row = (top + bot) // 2
if target > matrix[row][-1]:
top = row + 1
elif target < matrix[row][0]:
bot = row - 1
else:
break
if not (top <= bot):
return False
row = (top + bot) // 2
l, r = 0, COLS - 1
while l <= r:
m = (l + r) // 2
if target > matrix[row][m]:
l = m + 1
elif target < matrix[row][m]:
r = m - 1
else:
return True
return False
JavaScript
class Solution {
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
searchMatrix(matrix, target) {
const ROWS = matrix.length;
const COLS = matrix[0].length;
let top = 0;
let bot = ROWS - 1;
while (top <= bot) {
const row = Math.floor((top + bot) / 2);
if (target > matrix[row][COLS - 1]) {
top = row + 1;
} else if (target < matrix[row][0]) {
bot = row - 1;
} else {
break;
}
}
if (!(top <= bot)) {
return false;
}
const row = Math.floor((top + bot) / 2);
let l = 0;
let r = COLS - 1;
while (l <= r) {
const m = Math.floor((l + r) / 2);
if (target > matrix[row][m]) {
l = m + 1;
} else if (target < matrix[row][m]) {
r = m - 1;
} else {
return true;
}
}
return false;
}
}
4. Binary Search(One Pass) Method
Perform binary search directly on the matrix using row and column calculations in a single pass, avoiding flattening.
- Time complexity: O(log (m*n))
- Space complexity: O(1)
where m is the number of rows and n is the number of columns of matrix.
Code
C++
Java
Python
JavaScript
C++
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int ROWS = matrix.size(), COLS = matrix[0].size();
int l = 0, r = ROWS * COLS - 1;
while (l <= r) { int m = l + (r - l) / 2; int row = m / COLS, col = m % COLS; if (target > matrix[row][col]) {
l = m + 1;
} else if (target < matrix[row][col]) {
r = m - 1;
} else {
return true;
}
}
return false;
}
};
Java
public class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int ROWS = matrix.length, COLS = matrix[0].length;
int l = 0, r = ROWS * COLS - 1;
while (l <= r) {
int m = l + (r - l) / 2;
int row = m / COLS, col = m % COLS;
if (target > matrix[row][col]) {
l = m + 1;
} else if (target < matrix[row][col]) {
r = m - 1;
} else {
return true;
}
}
return false;
}
}
Python
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
ROWS, COLS = len(matrix), len(matrix[0])
l, r = 0, ROWS * COLS - 1
while l <= r:
m = l + (r - l) // 2
row, col = m // COLS, m % COLS
if target > matrix[row][col]:
l = m + 1
elif target < matrix[row][col]:
r = m - 1
else:
return True
return False
JavaScript
class Solution {
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
searchMatrix(matrix, target) {
let ROWS = matrix.length, COLS = matrix[0].length;
let l = 0, r = ROWS * COLS - 1;
while (l <= r) {
let m = l + Math.floor((r - l) / 2);
let row = Math.floor(m / COLS), col = m % COLS;
if (target > matrix[row][col]) {
l = m + 1;
} else if (target < matrix[row][col]) {
r = m - 1;
} else {
return true;
}
}
return false;
}
}
