Reverse Nodes In K Group
Reverse Nodes In K Group Problem
You are given the head of a singly linked list and a positive integer k.
Reverse the first k nodes of the list, then reverse the next k nodes, and continue this process. If there are fewer than k nodes remaining, leave them as is.
Return the updated linked list with nodes reversed in groups of k, modifying only the nodes’ next pointers, not their values.
Examples related Reverse Nodes in K Group
Example 1:
Illustration 1:
Input: head = [1,2,3,4,5,6], k = 3
Output: [3,2,1,6,5,4]
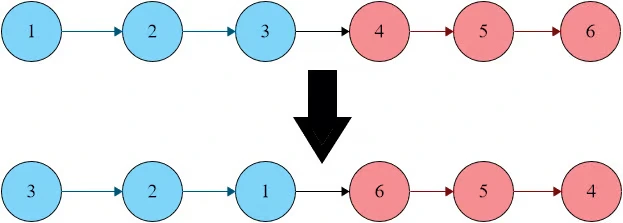
Output: [3,2,1,6,5,4]
Example 2:
Example 2:
Input: head = [1,2,3,4,5], k = 3
Output: [3,2,1,4,5]
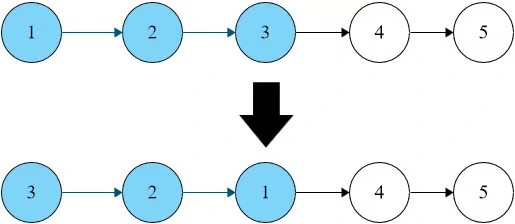
Output: [3,2,1,4,5]
Constraints:
- Length of the linked list is n.
- 1 <= k <= n <= 100
- 0 <= Node.val <= 100
Hints to Solve Reverse Nodes In K Group
Hint 1 :
Brute-force approach would involve storing node values in an array, reversing the groups one by one, and then converting it back to a linked list, which takes O(n) space.
Can you think of a more efficient way, perhaps by reversing the linked list in place without extra space?
Hint 2 :
- We can reverse each group in place and keep track of the head of the next group.
- For example, with a list like [1, 2, 3, 4, 5] and k = 2, we reverse [1, 2] to [2, 1], then [3, 4] to [4, 3], while correctly linking 1 to 4 and 3 to 5.
- How can we efficiently manage these connections?
Hint 3 :
Use a dummy node to handle head modifications, pointing its next pointer to the current head.
Iterate k nodes, saving the next group’s head, and track the tail of the previous group.
After reversing the current group, reconnect the previous tail to the new head, and the current tail to the next group’s head.
Repeat this for all groups and return the new head of the list.
Recommendation for Time and Space Complexity (For Reverse Nodes In K Group)
Aim for a solution with O(n) time and O(1) space, where n is the length of the list.
There are mainly 2 approach to solve Reverse Nodes In K Group problem:
- Recursion Method
- Iteration Method
1. Recursion Method
- In this approach, we recursively reverse the nodes in k-group chunks.
- At each step, we reverse the first k nodes and then move to the next group.
- Once we reach a group with fewer than k nodes, we stop and return the modified list.
- Time complexity: O(n)
- Space complexity: O(n/k)
Code:
C++
Java
Python
JavaScript
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* cur = head;
int group = 0;
while (cur != nullptr && group < k) {
cur = cur->next;
group++;
}
if (group == k) {
cur = reverseKGroup(cur, k);
while (group-- > 0) {
ListNode* tmp = head->next;
head->next = cur;
cur = head;
head = tmp;
}
head = cur;
}
return head;
}
};
Java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
public class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode cur = head;
int group = 0;
while (cur != null && group < k) {
cur = cur.next;
group++;
}
if (group == k) {
cur = reverseKGroup(cur, k);
while (group-- > 0) {
ListNode tmp = head.next;
head.next = cur;
cur = head;
head = tmp;
}
head = cur;
}
return head;
}
}
Python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
cur = head
group = 0
while cur and group < k:
cur = cur.next
group += 1
if group == k:
cur = self.reverseKGroup(cur, k)
while group > 0:
tmp = head.next
head.next = cur
cur = head
head = tmp
group -= 1
head = cur
return head
JavaScript
/**
* Definition for singly-linked list.
* class ListNode {
* constructor(val = 0, next = null) {
* this.val = val;
* this.next = next;
* }
* }
*/
class Solution {
/**
* @param {ListNode} head
* @param {number} k
* @return {ListNode}
*/
reverseKGroup(head, k) {
let cur = head;
let group = 0;
while (cur && group < k) {
cur = cur.next;
group++;
}
if (group === k) {
cur = this.reverseKGroup(cur, k);
while (group-- > 0) {
let tmp = head.next;
head.next = cur;
cur = head;
head = tmp;
}
head = cur;
}
return head;
}
}
2. Iteration Method
- Iteration method involves reversing k nodes in a group iteratively.
- For each group, we reverse the nodes one by one while keeping track of the necessary pointers to reconnect the groups.
- This approach avoids recursion and works in-place.
- Time complexity: O(n)
- Space complexity: O(1)
Code:
C++
Java
Python
JavaScript
C++
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* dummy = new ListNode(0, head);
ListNode* groupPrev = dummy;
while (true) {
ListNode* kth = getKth(groupPrev, k);
if (!kth) {
break;
}
ListNode* groupNext = kth->next;
ListNode* prev = kth->next;
ListNode* curr = groupPrev->next;
while (curr != groupNext) {
ListNode* tmp = curr->next;
curr->next = prev;
prev = curr;
curr = tmp;
}
ListNode* tmp = groupPrev->next;
groupPrev->next = kth;
groupPrev = tmp;
}
return dummy->next;
}
private:
ListNode* getKth(ListNode* curr, int k) {
while (curr && k > 0) {
curr = curr->next;
k--;
}
return curr;
}
};
Java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
ListNode dummy = new ListNode(0, head);
ListNode groupPrev = dummy;
while (true) {
ListNode kth = getKth(groupPrev, k);
if (kth == null) {
break;
}
ListNode groupNext = kth.next;
ListNode prev = kth.next;
ListNode curr = groupPrev.next;
while (curr != groupNext) {
ListNode tmp = curr.next;
curr.next = prev;
prev = curr;
curr = tmp;
}
ListNode tmp = groupPrev.next;
groupPrev.next = kth;
groupPrev = tmp;
}
return dummy.next;
}
private ListNode getKth(ListNode curr, int k) {
while (curr != null && k > 0) {
curr = curr.next;
k--;
}
return curr;
}
}
Python
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
dummy = ListNode(0, head)
groupPrev = dummy
while True:
kth = self.getKth(groupPrev, k)
if not kth:
break
groupNext = kth.next
prev, curr = kth.next, groupPrev.next
while curr != groupNext:
tmp = curr.next
curr.next = prev
prev = curr
curr = tmp
tmp = groupPrev.next
groupPrev.next = kth
groupPrev = tmp
return dummy.next
def getKth(self, curr, k):
while curr and k > 0:
curr = curr.next
k -= 1
return curr
JavaScript
/**
* Definition for singly-linked list.
* class ListNode {
* constructor(val = 0, next = null) {
* this.val = val;
* this.next = next;
* }
* }
*/
class Solution {
/**
* @param {ListNode} head
* @param {number} k
* @return {ListNode}
*/
reverseKGroup(head, k) {
const dummy = new ListNode(0, head);
let groupPrev = dummy;
while (true) {
const kth = this.getKth(groupPrev, k);
if (!kth) {
break;
}
const groupNext = kth.next;
let prev = kth.next;
let curr = groupPrev.next;
while (curr != groupNext) {
const tmp = curr.next;
curr.next = prev;
prev = curr;
curr = tmp;
}
const tmp = groupPrev.next;
groupPrev.next = kth;
groupPrev = tmp;
}
return dummy.next;
}
getKth(curr, k) {
while (curr && k > 0) {
curr = curr.next;
k--;
}
return curr;
}
}
