2 Eggs and 100 Floors Puzzle
Puzzle - 2 Eggs and 100 Floors
Given below are a puzzle based on 2 eggs and 100 floors building. Let’s see the following:
There is a 100 floors building.
There are two possible scenes we need to analyze:
- If an egg drops from the N’th floor or above it will break.
- If it’s dropped from any floor below ‘N’, it will not break
Note: You’re given only 2 eggs
Questions:
1 – Find the N’th floor.
2 – How many drops do you need to make?
3 – What should be the best strategy to minimize the number of egg drops?
Puzzle - 2 Eggs and 100 Floors
Solving 2 Eggs and 100 Floors Puzzle
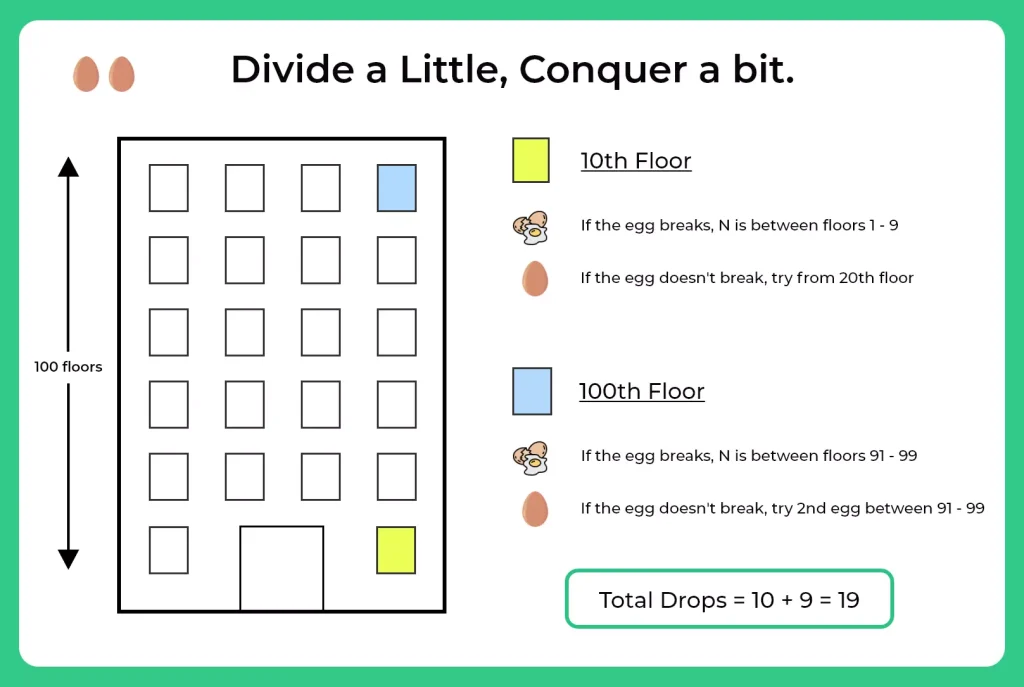
Method 1: Divide a Little, Conquer a Bit:
Let’s start the method from the 10th floor and go up to 10 floors at a time.
What we have to do:
Step 1: Throw the egg from the 10th floor, and if it breaks, then we can conclude that the ‘N’ floor is between 1-9.
Step 2: Repeat the same process if the egg is unbroken on the 10th, and now throw it from the 20th floor. Repeat the process until the 100th floor.
Step 3: So, even if the first egg is unbroken, we can now try the second egg and throw it from floors 91 – 99.
Let’s count the drops:
- 10 drops on each 10th floor (1 – 100)
- 9 drops in between the floors (91 – 99)
So, the number of drops in the worst-case scenario is 19.
Method 2: Balancing Linear Drops:
Let’s assume the egg breaks at floor N.
We try to find out by going (N-1) to the first floor by doing the linear search.
To find an optimum solution, let’s try this:
If for every N, the egg doesn’t break, go to (N-1). This would save us one drop as we are doing a linear search with the second egg when egg 1 breaks.
=> So the series would look something like this ——————-> N + (N – 1) + (N – 2) + (N – 3) +……+ 1
=> Now this is a series which gives us an equation as ———> n\frac{\left(n-1\right)}{2}
=> Now, since it is given that the egg may or may not break from the 100th floor.
We can write it as.
n\frac{\left(n-1\right)}{2}>=100
= 13.651 or 14 (approx)
N = 14
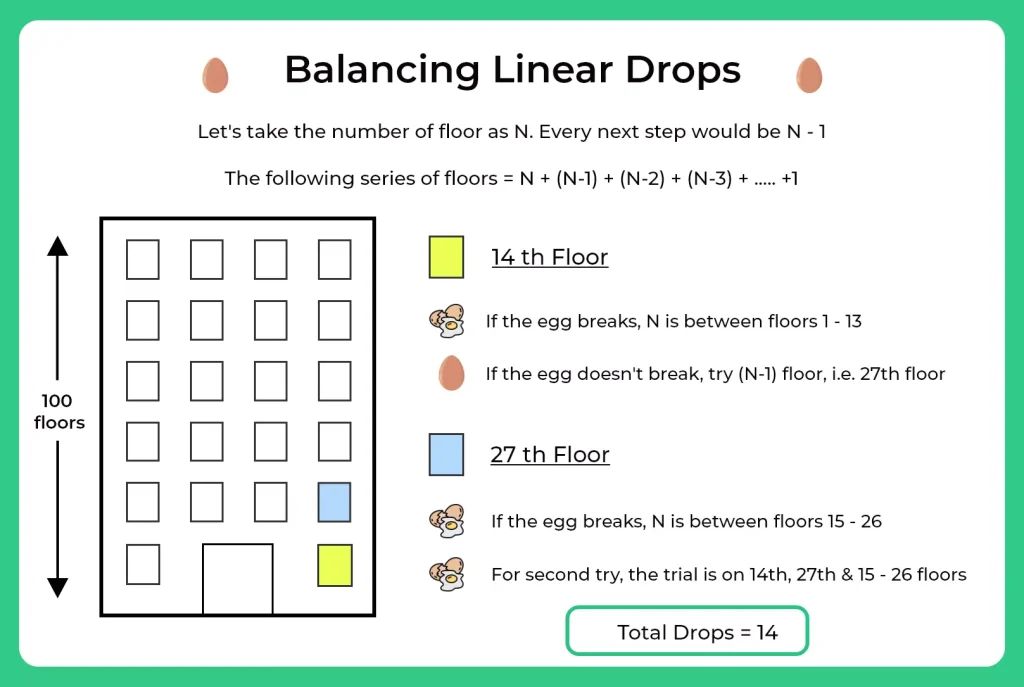
Implementation:
Step 1: We should start from the 14th floor and then move up (N – 1) 13 floors i.e. 27th floor.
Step 2: If the eggs break on the 14th floor, try from all the floors below it, i.e. (1 – 13)
Step 3: Following the same linear pattern, we can move to (N – 2), (N – 3), and so on.
Step 4: So the floors from where the drop needs to be done are: 14, 27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100
Let’s count the number of drops:
- Dropping from 14 and if it breaks then dropping from 1 – 13
- Dropping from 14 and if unbroken, then trying from floor 27. If it breaks then try it from 15 – 26.
- So you have now tried on the 14th and 27th floor along with 15 – 26. So total of 14 floors.
- This continues with every attempt.
So, the number of drops in the worst-case scenario is 14.
Result:
Answer 1 – N is 14
Answer 2 – The total number of drops we need to make is 14
Answer 3 – The strategy we need to adopt is Balancing Linear Drops,
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
- Crossing the Bridge Puzzle Answer
- Death & Marbles Puzzle Answer
- Airplane Seat Puzzle Answer
- Bank Cashier Puzzle Answer
- Calendar Cube Puzzle Answer
- Ants & Triangle Puzzle Answer
- Measuring 9 mins Puzzle Answer
- Bulb in a Circle Puzzle Answer
- Camel & Bananas Puzzle Answer
- King & Wine Puzzle Answer
- Sum & Product Puzzle Answer
- Heaven or Hell Puzzle Answer
- 3 Mislablled Jars Puzzle Answer
Login/Signup to comment