Deletion in B-Tree

B-Trees
In this article, we will learn Introduction to B-Trees. B-Tree is a self-balancing search tree. The main idea of using B-Trees is to reduce the number of disk accesses. The height of B-Trees is kept low by putting maximum possible keys in a B-Tree node.
Deletion in B-Tree
In this article, we will learn about Deletion in B-Tree.
- Deletion from a B-tree is more complicated than insertion
- We can delete a key from any node and when we delete a key from an internal node, we will have to rearrange the node’s children.
- We must make sure that deletion process doesn’t violate the B-tree properties.
- We must ensure that a node doesn’t get too small during deletion (except that the root is allowed to have fewer than the minimum number n-1 of keys, where n is the degree).
- For deletion, we follow such an approach which might have to back up if a node along the path to where the key is to be deleted has the minimum number of keys.
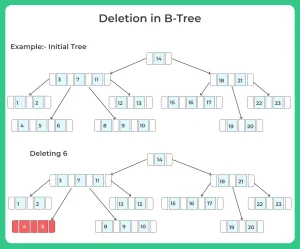
Various Cases of Deletion
Case 1.
If the key k is in node x and x is a leaf, delete the key k from x.
Case 2
If the key k is in node x and x is an internal node, do the following.
- If the child y that precedes k in node x has at least n keys, then find the predecessor k0 of k in the sub-tree rooted at y. Recursively delete k0, and replace k with k0 in x. (We can find k0 and delete it in a single downward pass.)
- If y has fewer than n keys, then, symmetrically, examine the child z that follows k in node x. If z has at least n keys, then find the successor k0 of k in the subtree rooted at z. Recursively delete k0, and replace k with k0 in x. (We can find k0 and delete it in a single downward pass.)
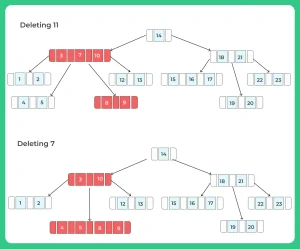
- Otherwise, if both y and z have only n-1 keys, merge k and all of z into y, so that x loses both k and the pointer to z, and y now contains 2n-1 keys. Then free z and recursively delete k from y.
Case 3
If the key k is not present in internal node x, determine the root x.c(i) of the appropriate subtree that must contain k, if k is in the tree at all. If x.c(i) has only n-1 keys, execute step 1 or 2 in this case as necessary to guarantee that we descend to a node containing at least n keys. Then finish by recursing on the appropriate child of x.
- If x.c(i) has only n-1 keys but has an immediate sibling with at least n keys, give x.c(i) an extra key by moving a key from x down into x.c(i), moving a key from x.c(i) ’s immediate left or right sibling up into x,and moving the appropriate child pointer from the sibling into x.c(i).
- If x.c(i) and both of x.c(i)’s immediate siblings have n-1 keys, merge x.c(i) with one sibling, which involves moving a key from x down into the new merged node to become the median key for that node.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others





Login/Signup to comment