Sort Array in Waveform in C
Sort Array in Waveform in C Programming Language
This page is all about converting an array into a waveform. To convert an array in waveform we can use two concepts.
- Brute Force Solution — Using Sorting
- Incrementing the loop by two
we will be learning about both of them in this page, their working and C program.

Sort Array in Waveform in C Language
A waveform sorted array is an array of integers that has been sorted in a specific way to resemble a waveform. In this sorting method, the elements in the array are arranged in a “peak-valley” pattern, where the first element is the peak, the second element is the valley, the third element is the peak again, and so on.
For example, consider the following waveform sorted array:
[10, 5, 6, 2, 20, 3, 48, 30]
In this array, the first element 10 is the peak, the second element 5 is the valley, the third element 6 is the peak again, the fourth element 2 is the valley, the fifth element 20 is the peak and so on.
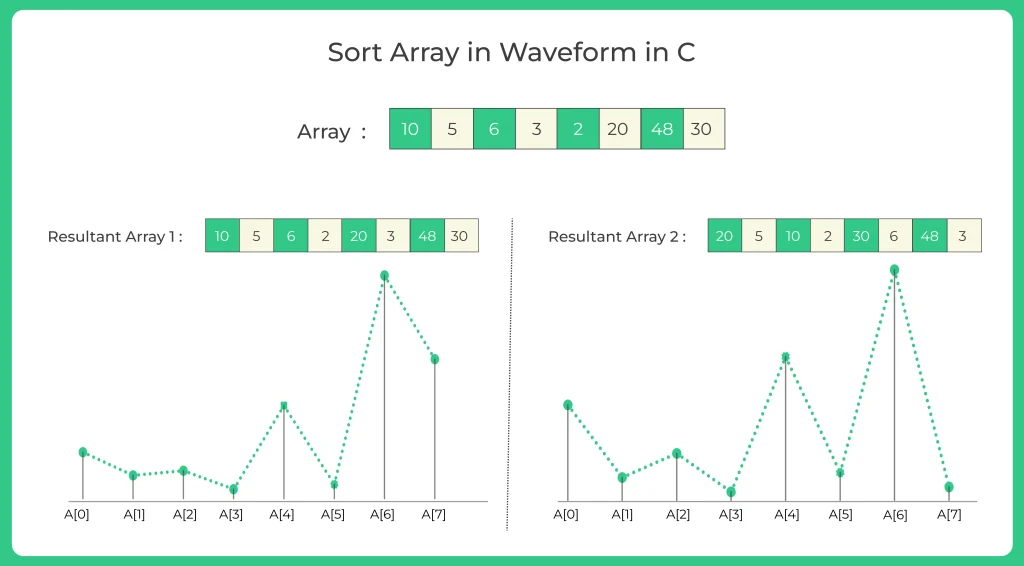
The advantage of using a waveform sorted array is that it allows for efficient searching and sorting algorithms. For example, a binary search algorithm can be used to search for an element in the array with a time complexity of O(log n), which is much faster than a linear search algorithm with a time complexity of O(n). Similarly, the array can be sorted using a modified version of a merge sort algorithm that takes advantage of the waveform pattern, resulting in a time complexity of O(n log n).
In summary, a waveform sorted array is a specific way of sorting an array of integers to resemble a waveform, which allows for efficient searching and sorting algorithms.
Method 1 : Brute Force Solution (using sorting)
This is a simple method of solving this question which contains basic 2 steps and they are as follow
Step : 1 – Sort the array in ascending order.
Step : 2 – Swap all adjacent elements of the array
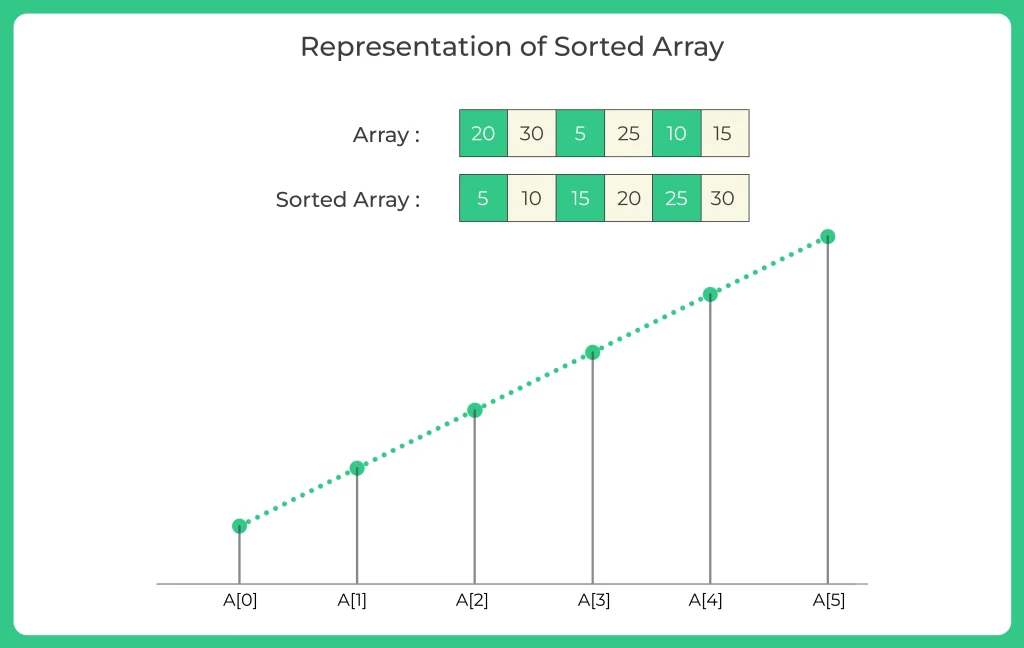
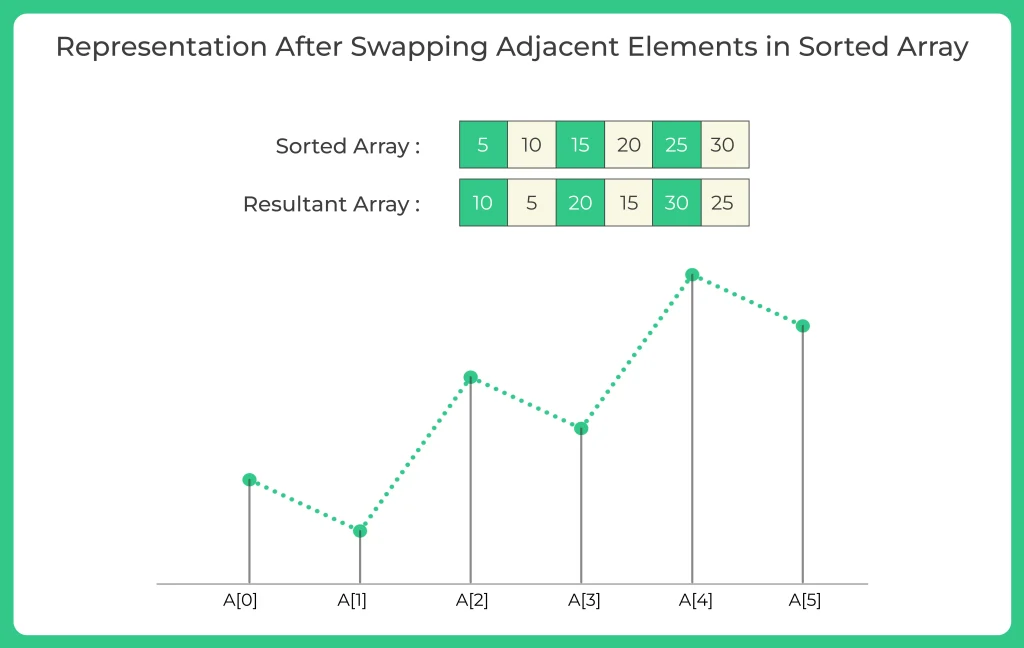
Let us consider the input array be {20, 30, 5, 25, 10, 15}. After sorting, we get {5, 10, 15, 20, 25, 30}. After swapping adjacent elements, we get {10, 5, 20, 15, 30, 25}.
If we plot step 1 (that is sorted array) on graph then it would look something like this.
If we plot step 2 (that is swapping adjacent elements) on graph then it would look something like this.
Method : 1 -Solution in C Programming Language
#include<stdio.h>
int main ()
{
int array[] = { 10, 49, 2, 1, 5, 23 };
int n = sizeof (array) / sizeof (array[0]);
int temp;
for (int i = 0; i < n - 1; i++)
{
for (int j = i + 1; j < n; j++) { if (array[i] > array[j])
{
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
}
//step 2
for (int i = 0; i < n; i = i + 2)
{
temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
//printing result
for (int i = 0; i < n; i++)
{
printf ("%d ", array[i]);
}
return 0;
}
Output
2 1 10 5 49 23
Method 2 : Incrementing the loop by 2
The complexity of method used above is O(nLogn) which is used in the algorithms like heap sort etc. This question can be solved in O(n) complexity using single traverse of array.
Following are the steps which will be used to solve this program in O(n) complexity.
Main step : Traverse all even position elements of array (i.e. at index 0, 2, 4, 6, 8 – – -)
Condition 1 : If current element is smaller than previous odd element, swap previous and current.
Condition 2 : If current element is smaller than next odd element, swap next and current.
Method: 2 – Solution in C Programming Language
#include<stdio.h>
int main ()
{
int array[] = { 10, 49, 2, 1, 5, 23 };
int n = sizeof (array) / sizeof (array[0]);
int temp;
for (int i = 0; i < n; i = i + 2)
{
if (i > 0 && array[i - 1] > array[i])
{
temp = array[i];
array[i] = array[i - 1];
array[i - 1] = temp;
}
if (i < n - 1 && array[i] < array[i + 1])
{
temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
for (int i = 0; i < n; i++)
{
printf ("%d ", array[i]);
}
return 0;
}
Output
49 2 10 1 23 5



Dear prepinsta, please try to solve this question with odd number of elements