Majority Element in an Array in C
Majority Element in array in C Language
In this page we will look into a coding question where we will learn how to find the element which occurs majority number of times in array in C Programming Language.
There might be different approach to solve this question, one you will find here. If your approach is bit different post it onto the comment section.
Majority Element In An Array In C
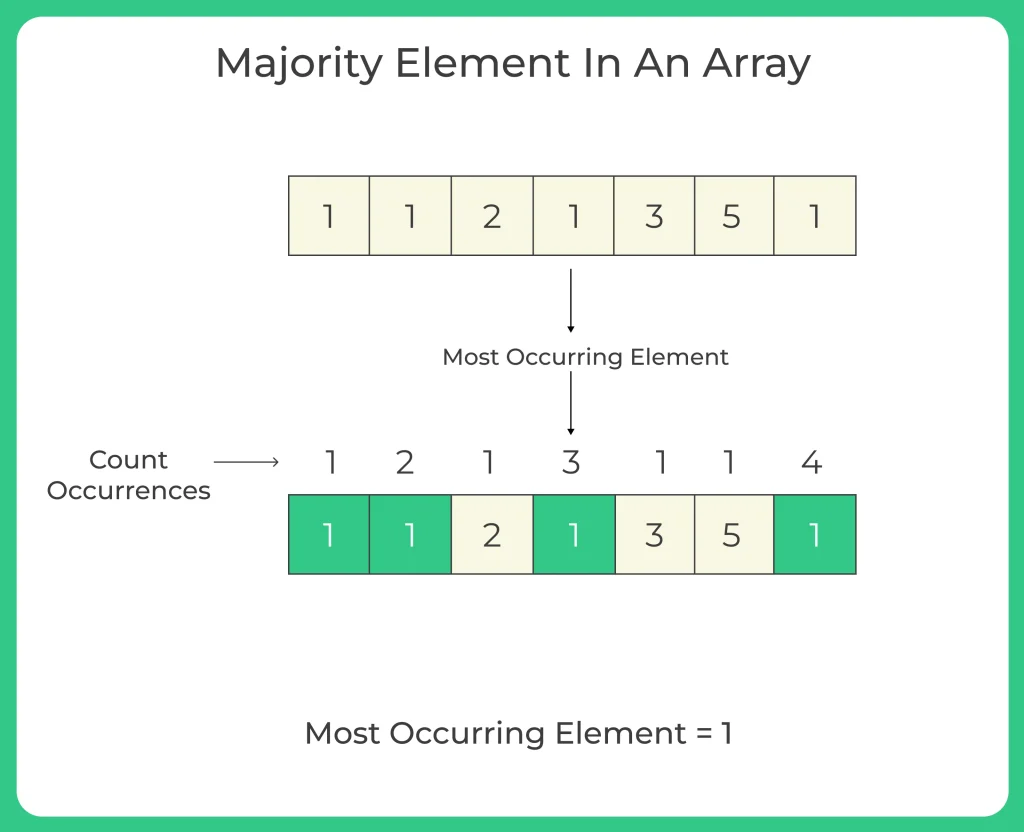
- The majority element in an array is one that appears more than n/2 times in an array of size n. There are various algorithms that can be used to find the major element.
- One such algorithm is Moore’s Voting Algorithm, which works through two-passes; it first finds a potential candidate by counting its frequency, and then verifies it by counting it again on the second pass.
- Alternatively, one can use a hash table to count each element’s frequency and find the majority element from that.
- Lastly, sorting the array and checking its middle element can work too, though this has a time complexity of O(nlogn).
- Overall, Moore’s Voting Algorithm is regarded as the most efficient given its O(n) time complexity and O(1) space complexity.
Algorithm
- Start
- set maxCount=0, Index=-1
- Start loop from i=0 to i < n
- set count = 0
- Start loop from j=0 to j < n
- if(arr[i]==arr[j])
- count++
- End if
- End For
- Start if (count > maxCount)
- maxCount = count
- index = i
- End If
- End For
- Start if (maxCount > n / 2)
- print arr[index]
- End if
- Else print “No Majority Element”
- End Else
- Stop
Program for finding the element that occurs most time in an array
Run
#include<stdio.h>
void getMajorityElement(int arr[], int n)
{
int maxCount = 0;
int index = -1; // sentinels
for (int i = 0; i < n; i++) {
int count = 0;
for (int j = 0; j < n; j++) {
if (arr[i] == arr[j])
count++;
}
// update maxCount if count of
// current element is greater
if (count > maxCount) {
maxCount = count;
index = i;
}
}
// if maxCount is greater than n/2
// return the corresponding element
if (maxCount > n / 2)
printf("Majority Element = %d\n",arr[index]);
else
printf("No Majority Element\n");
}
// Driver code
int main()
{
int arr[] = { 3, 3, 4, 2, 4, 4, 2, 4, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
// Function calling
getMajorityElement(arr, n);
return 0;
}
Output
Majority Element = 4
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Login/Signup to comment
/********************************************
#include
int main()
{
int n;
scanf(“%d”,&n);
int array[n];
int max = 0;
int count;
int maxelement;
for(int i=0; i<n; i++)
{
scanf("%d",&array[i]);
}
for(int i=0; i<n; i++)
{
count=0;
for(int j=0; j1)
{
max = count;
maxelement = array[i];
}
}
printf(“%d”,maxelement);
return 0;
}