Pythagorean Triplet in an Array in C

May 2, 2023

Pythagorean Triplet in C

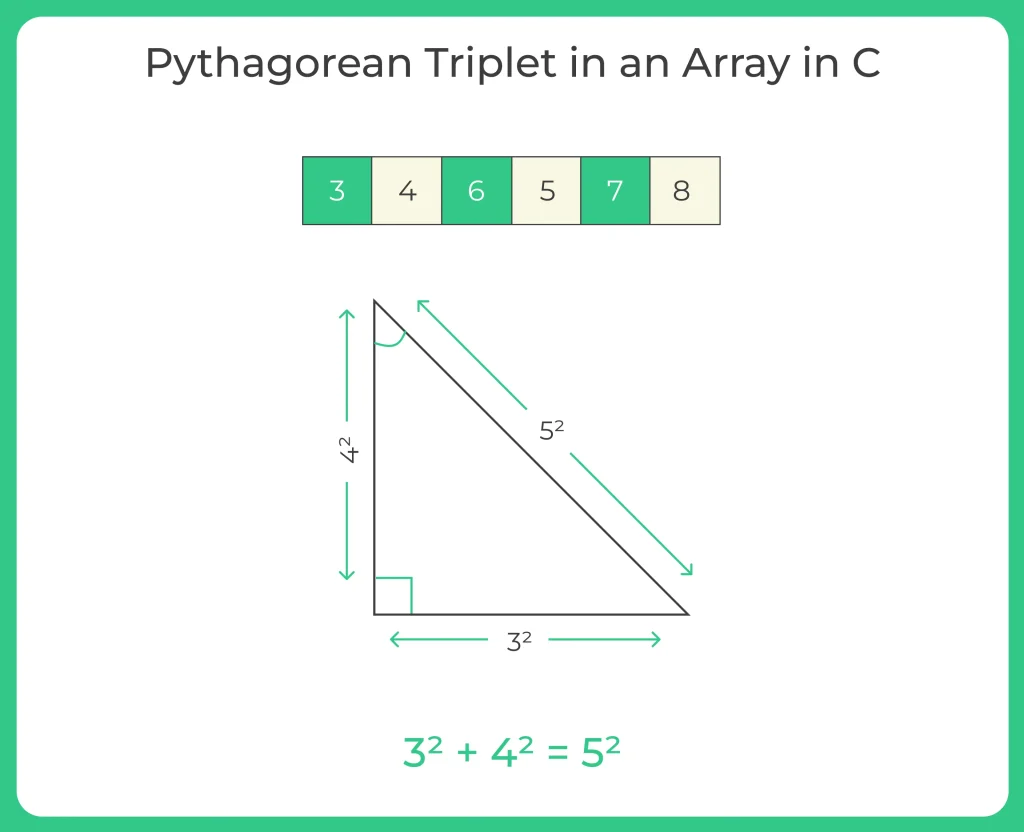
A Pythagorean triple consists of three positive integers a, b, and c, such that a² + b² = c². Such a triple is commonly written, and a well-known example is. If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are co-prime.

In this page we will look into a program to find Pythagorean Triplet in an Array in C .

Pythagorean Triplet in an Array in C

Pythagorean Triplet in an Array in C

We have to find the set of Pythagorean triples from the given array that satisfies pythagorean triplet condition . On this page we will discuss two methods to solve this problem.
  1. Brute Force (Time complexity: O(n^3) )
  2. Using Sorting (Time complexity: O(n^2) )
Pythagorean Triplet in an Array in C

Algorithm For Brute Force Method

  1. We use 3 loops such that we take set of 3 different elements from the array.
    1. We run 3 for loops. Such that for every a we take all the values b except itself. For every b we take all the values of a.
    2. a, b, c are elements from the array.
  2. we run the Pythagorean condition that is a*a + b*b = c*c, for all the sets of (a, b, c). we print them when it is true.
    1. If a^2 + b^2 = c^2, print a, b, c.
DSA desktop gif
DSA mobile gif

Introduction to 2-D Arrays

Reverse an array or string

Find pairs in array with given sum

Sort the array in Waveform

Boyer-Moore’s Voting Algorithm

Method 1 :Brute Force

Run 
#include <stdio.h>
 
int isTriplet(int arr[], int n) 
{ 
    int x, y, z;
    for (int i = 0; i < n; i++) 
    { 
        for (int j = i + 1; j < n; j++) 
        { 
            for (int k = j + 1; k < n; k++) 
            { 
                // Calculate square of array elements 
                x = arr[i] * arr[i], y = arr[j] * arr[j], z = arr[k] * arr[k]; 
                if (x == y + z || y == x + z || z == x + y)
                {
                    printf("%d, %d, %d",arr[i],arr[j],arr[k]);
                    return 1; 
                }   
            } 
        } 
    } 
  
    // If we reach here, no triplet found 
    return -1; 
} 
  
/* Driver program to test above function */
int main() 
{ 
    int arr[]={3,4,6,5,7,8};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    int result = isTriplet(arr,n);
    if(result == -1)
    {
        printf("no triples found");
    } 
    return 0; 
}

Output

3, 4, 5

Algorithm For Sorting Method

  1. Sort the given array in ascending order.
  2. Iterate over the array and for each element, find its square.
  3. Initialize two pointers, left and right, at positions 0 and n-1 respectively, where n is the size of the array.
  4. While left < right, check if the sum of squares of elements at left and right pointers is equal to the square of the current element. If so, we have found a Pythagorean triplet and we can return true. If the sum is less than the square, move the left pointer to the right. If the sum is greater than the square, move the right pointer to the left.
  5. If we exhaust all possible combinations of left and right pointers and do not find a Pythagorean triplet, return false.

Method 2 : Using Sorting

Run 
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <math.h>

int cmpfunc (const void *a, const void *b)
{
  return (*(int *) a - *(int *) b);
}

void isTriplet (int arr[], int n)
{
  // Step 1
  for (int i = 0; i < n; i++)
    arr[i] = arr[i] * arr[i];

  // Sort array elements 
  qsort (arr, n, sizeof (int), cmpfunc);

  // Step 2 and Step 3 
  for (int i = n - 1; i >= 2; i--)
    {				// Fixing a
      int b = 0;		// Fixing b
      int c = i - 1;		// Fixing c
      while (b < c)
	{
	  // A triplet found 
	  if (arr[b] + arr[c] == arr[i])
	    {
	      int x = sqrt (arr[b]);
	      int y = sqrt (arr[c]);
	      int z = sqrt (arr[i]);

	      printf ("%d, %d, %d \n", x, y, z);
	      b++;
	      c--;
	    }

	  // Else either move 'b' or 'c' 
	  else if (arr[b] + arr[c] < arr[i])
	    {
	      b++;
	    }
	  else
	    {
	      c--;
	    }
	}
    }
}

// Driver code
int main ()
{
  int arr[] = { 3, 4, 6, 5, 7, 8 };
  int n = sizeof (arr) / sizeof (arr[0]);
  isTriplet (arr, n);
  return 0;
}

Output

3, 4, 5

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime

Get over 200+ course One Subscription

Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others

Get Prime
Course List
Course List

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout list of all the video courses in PrepInsta Prime Subscription

Checkout
Checkout

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion : C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal Line by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric – C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree- C | C++ | Java

Introduction to Trees

Binary Trees

Binary Search Trees

Traversals

  • Traversal in Trees
  • Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
  • Tree Traversals: Depth First Search (DFS) : C | C++ | Java
  • Construct a Binary Tree from Postorder and Inorder

B – Trees

AVL Trees

  • AVL Trees
    • AVL Trees: Introduction
    • AVL Tree Insertion :  C | C++ | Java
    • AVL Tree Deletion : C | C++ | Java
    • Insertion in a Binary Tree (Level Order) – C | C++ | Java
    • Searching in Binary Tree – C | C++ | Java
    • Searching in a Binary Search Tree – C | C++ | Java

Complete Programs for Trees

  • Depth First Traversals – C | C++ | Java
  • Level Order Traversal – C | C++ | Java
  • Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
  • Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
  • Find size of the Binary tree – C | C++ | Java
  • Find the height of binary tree – C | C++ | Java
  • Find maximum in binary tree – C | C++ | Java
  • Check whether two tree are identical- C| C++| Java
  • Spiral Order traversal of Tree- C | C++| Java
  • Level Order Traversal LIne by Line – C | C++| Java
  • Hand shaking lemma and some Impotant Tree Properties.
  • Check If binary tree if Foldable or not.- C| C++| Java
  • check whether tree is Symmetric  C| C++| Java.
  • Check for Children-Sum in Binary Tree- C|C++| Java
  • Sum of all nodes in Binary Tree- C | C++ | Java
  • Lowest Common Ancestor in Binary Tree. C | C++ | Java