Uber Coding Questions and Answers

March 27, 2025

Uber Coding Questions with Solutions

Here on this page you will get Sample Uber coding questions and answers which will help you to prepare for Online Coding Assessment of Uber to hire freshers for SDE 1 Role.

Let you know that the Online Assessment will be conducted on CodeSignal Platform. After Application Process, candidates will be communicated through mail for Online Assessment on CodeSignal.

Uber SDE 1 Profile Details

Role: Software Development Engineer 1 (SDE 1)
Work:

Develop, test, and maintain scalable software solutions.
Collaborate with teams to build high-performance applications.
Solve real-world engineering challenges using algorithms and data structures.

Tech Stack Required:

Programming Languages: Python, Java, C++, Go
Data Structures & Algorithms (DSA)
Databases: SQL, NoSQL (MongoDB, Cassandra)
Backend: Microservices, REST APIs
Frontend (if required): React, Angular
Cloud & DevOps: AWS, Kubernetes, Docker (preferred)

Checkout PrepInsta Prime:

Practice Coding Questions:

Further on this page you will get Sample Uber Coding Questions and Answers that will help you to prepare for Uber Online Coding Assessment on CodeSignal Platform.

Sample Uber Coding Questions with Solutions

Question 1: Finding Longest Repeating Character Replacement Problem

You are given a string s that contains only uppercase English letters and an integer k. Your task is to determine the length of the longest substring in s that can consist of just one distinct character after modifying the string.

You are allowed to make up to k replacements, where each replacement involves changing any character in the substring to another uppercase English letter.

The goal is to maximize the length of this uniform substring by carefully choosing which characters to replace while staying within the limit of k changes.

Example: Input: s = "AAABABB", k = 1
Output: 5

Constraints:

1 <= s.length <= 1000
0 <= k <= s.length

Solving Through Sliding Window Method

Maintain a sliding window and expand it to include more characters. If the number of characters to replace exceeds the limit, shrink the window from the left. Track the longest valid window during this process.

Time complexity: O(m*n)
Space complexity: O(m)

where n is the length of the string and m is the total number of unique characters in the string.

Code

C++

Java

Python

JavaScript

C++

class Solution {
public:
    int characterReplacement(std::string s, int k) {
        int res = 0;
        unordered_set charSet(s.begin(), s.end());

        for (char c : charSet) {
            int count = 0, l = 0;
            for (int r = 0; r < s.size(); r++) {
                if (s[r] == c) {
                    count++;
                }

                while ((r - l + 1) - count > k) {
                    if (s[l] == c) {
                        count--;
                    }
                    l++;
                }

                res = std::max(res, r - l + 1);
            }
        }
        return res;
    }
};

Java

public class Solution {
    public int characterReplacement(String s, int k) {
        int res = 0;
        HashSet charSet = new HashSet<>();
        for (char c : s.toCharArray()) {
            charSet.add(c);
        }

        for (char c : charSet) {
            int count = 0, l = 0;
            for (int r = 0; r < s.length(); r++) {
                if (s.charAt(r) == c) {
                    count++;
                }

                while ((r - l + 1) - count > k) {
                    if (s.charAt(l) == c) {
                        count--;
                    }
                    l++;
                }

                res = Math.max(res, r - l + 1);
            }
        }
        return res;
    }
}

Python

class Solution:
    def characterReplacement(self, s: str, k: int) -> int:
        res = 0
        charSet = set(s)

        for c in charSet:
            count = l = 0
            for r in range(len(s)):
                if s[r] == c:
                    count += 1

                while (r - l + 1) - count > k:
                    if s[l] == c:
                        count -= 1
                    l += 1
                    
                res = max(res, r - l + 1)
        return res

JavaScript

class Solution {
    /**
     * @param {string} s
     * @param {number} k
     * @return {number}
     */
    characterReplacement(s, k) {
        let res = 0;
        let charSet = new Set(s);

        for (let c of charSet) {
            let count = 0, l = 0;
            for (let r = 0; r < s.length; r++) {
                if (s[r] === c) {
                    count++;
                }

                while ((r - l + 1) - count > k) {
                    if (s[l] === c) {
                        count--;
                    }
                    l++;
                }

                res = Math.max(res, r - l + 1);
            }
        }
        return res;
    }
}

Question 2: Serializing and Deserializing Binary Tree.

Create an algorithm to convert a binary tree into a string (serialization) and then reconstruct the same binary tree from that string (deserialization).

Serialization means converting a binary tree into a format that can be saved or sent to another system. Deserialization means converting that saved format back into the original binary tree.

Goal is to ensure that the binary tree can be serialized into a string and later deserialized back to its original structure without any loss of information. There are no specific rules for how you should implement this; the approach is up to you.

Example:

Example: Input: root = []
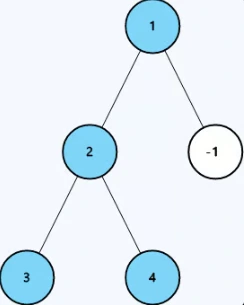
Output: []

Constraints:

0 <= The number of nodes in the tree <= 1000.
-1000 <= Node.val <= 1000

Solving Breadth First Search Method

In the BFS approach, the binary tree is serialized level by level using a queue to store node values. During deserialization, the data is processed sequentially to rebuild the tree by connecting child nodes level-wise.

Time complexity: O(n)
Space complexity: O(n)

Code

C++

Java

Python

JavaScript

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Codec {
public:

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        if (!root) return "N";
        string res;
        queue<TreeNode*> queue;
        queue.push(root);

        while (!queue.empty()) {
            TreeNode* node = queue.front();
            queue.pop();
            if (!node) {
                res += "N,";
            } else {
                res += to_string(node->val) + ",";
                queue.push(node->left);
                queue.push(node->right);
            }
        }
        return res;
    }

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        stringstream ss(data);
        string val;
        getline(ss, val, ',');
        if (val == "N") return nullptr;
        TreeNode* root = new TreeNode(stoi(val));
        queue<TreeNode*> queue;
        queue.push(root);

        while (getline(ss, val, ',')) {
            TreeNode* node = queue.front();
            queue.pop();
            if (val != "N") {
                node->left = new TreeNode(stoi(val));
                queue.push(node->left);
            }
            getline(ss, val, ',');
            if (val != "N") {
                node->right = new TreeNode(stoi(val));
                queue.push(node->right);
            }
        }
        return root;
    }
};

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if (root == null) return "N";
        StringBuilder res = new StringBuilder();
        Queu<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node == null) {
                res.append("N,");
            } else {
                res.append(node.val).append(",");
                queue.add(node.left);
                queue.add(node.right);
            }
        }
        return res.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] vals = data.split(",");
        if (vals[0].equals("N")) return null;
        TreeNode root = new TreeNode(Integer.parseInt(vals[0]));
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        int index = 1;

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (!vals[index].equals("N")) {
                node.left = new TreeNode(Integer.parseInt(vals[index]));
                queue.add(node.left);
            }
            index++;
            if (!vals[index].equals("N")) {
                node.right = new TreeNode(Integer.parseInt(vals[index]));
                queue.add(node.right);
            }
            index++;
        }
        return root;
    }
}

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Codec:
    
    # Encodes a tree to a single string.
    def serialize(self, root: Optional[TreeNode]) -> str:
        if not root:
            return "N"
        res = []
        queue = deque([root])
        while queue:
            node = queue.popleft()
            if not node:
                res.append("N")
            else:
                res.append(str(node.val))
                queue.append(node.left)
                queue.append(node.right)
        return ",".join(res)
        
    # Decodes your encoded data to tree.
    def deserialize(self, data: str) -> Optional[TreeNode]:
        vals = data.split(",")
        if vals[0] == "N":
            return None
        root = TreeNode(int(vals[0]))
        queue = deque([root])
        index = 1
        while queue:
            node = queue.popleft()
            if vals[index] != "N":
                node.left = TreeNode(int(vals[index]))
                queue.append(node.left)
            index += 1
            if vals[index] != "N":
                node.right = TreeNode(int(vals[index]))
                queue.append(node.right)
            index += 1
        return root

JavaScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     constructor(val = 0, left = null, right = null) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

class Codec {
    /**
     * Encodes a tree to a single string.
     *
     * @param {TreeNode} root
     * @return {string}
     */
    serialize(root) {
        if (!root) return "N";
        const res = [];
        const queue = new Queue();
        queue.push(root);

        while (!queue.isEmpty()) {
            const node = queue.pop();
            if (!node) {
                res.push("N");
            } else {
                res.push(node.val);
                queue.push(node.left);
                queue.push(node.right);
            }
        }
        return res.join(",");
    }

    /**
     * Decodes your encoded data to tree.
     *
     * @param {string} data
     * @return {TreeNode}
     */
    deserialize(data) {
        const vals = data.split(",");
        if (vals[0] === "N") return null;
        const root = new TreeNode(parseInt(vals[0]));
        const queue = new Queue([root]);
        let index = 1;

        while (!queue.isEmpty()) {
            const node = queue.pop();
            if (vals[index] !== "N") {
                node.left = new TreeNode(parseInt(vals[index]));
                queue.push(node.left);
            }
            index++;
            if (vals[index] !== "N") {
                node.right = new TreeNode(parseInt(vals[index]));
                queue.push(node.right);
            }
            index++;
        }
        return root;
    }
}

Question 3: N Queen Problem

The n-queens puzzle is about placing n queens on an n x n chessboard so that no two queens can attack each other.

Queens can attack in three ways: horizontally, vertically, and diagonally.

Your task is to find all possible ways to place the queens on the board, ensuring no two queens attack each other.

Each solution will show a unique board arrangement where ‘Q’ represents a queen and ‘.’ represents an empty square. The solutions can be returned in any order.

Example 1:

Input: n = 4
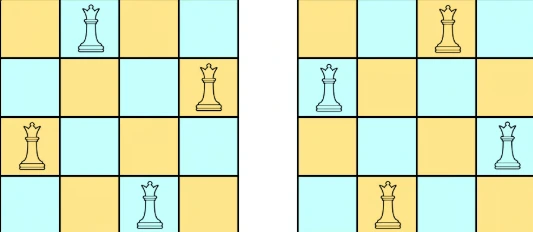
Output: [[".Q..","...Q","Q...","..Q."],
["..Q.","Q...","...Q",".Q.."]]
Explanation: There are two different solutions to the 4-queens puzzle.

Constraints:

1 <= n <= 8

Solving through Backtracking(Hash Set) Method

Here, we use hash sets to track the columns and diagonals already occupied by queens. These sets allow quick lookups to check if a cell is safe for placing a queen. The method reduces redundant checks and improves efficiency.

Time complexity: O(n!)
Space complexity: O(n^2)

Code

C++

Java

Python

JavaScript

C++

class Solution {
public:
    unordered_set<int> col;
    unordered_set<int> posDiag;
    unordered_set<int> negDiag;
    vector<vector<string>> res;

    vector<vector<string>> solveNQueens(int n) {
        vector<string> board(n, string(n, '.'));

        backtrack(0, n, board);
        return res;
    }

private:
    void backtrack(int r, int n, vector<string>& board) {
        if (r == n) {
            res.push_back(board);
            return;
        }

        for (int c = 0; c < n; c++) {
            if (col.count(c) || posDiag.count(r + c) || 
                negDiag.count(r - c)) {
                continue;
            }

            col.insert(c);
            posDiag.insert(r + c);
            negDiag.insert(r - c);
            board[r][c] = 'Q';

            backtrack(r + 1, n, board);

            col.erase(c);
            posDiag.erase(r + c);
            negDiag.erase(r - c);
            board[r][c] = '.';
        }
    }
};

Java

public class Solution {
    Set<Integer> col = new HashSet<>();
    Set<Integer> posDiag = new HashSet<>();
    Set<Integer> negDiag = new HashSet<>();
    List<List<String>> res = new ArrayList<>();
    
    public List<List<String>> solveNQueens(int n) {
        char[][] board = new char[n][n];
        for (char[] row : board) {
            Arrays.fill(row, '.');
        }

        backtrack(0, n, board);
        return res;
    }

    private void backtrack(int r, int n, char[][] board) {
        if (r == n) {
            List<String> copy = new ArrayList<>();
            for (char[] row : board) {
                copy.add(new String(row));
            }
            res.add(copy);
            return;
        }

        for (int c = 0; c < n; c++) {
            if (col.contains(c) || posDiag.contains(r + c) 
                || negDiag.contains(r - c)) {
                continue;
            }

            col.add(c);
            posDiag.add(r + c);
            negDiag.add(r - c);
            board[r][c] = 'Q';

            backtrack(r + 1, n, board);

            col.remove(c);
            posDiag.remove(r + c);
            negDiag.remove(r - c);
            board[r][c] = '.';
        }
    }
}

Python

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        col = set()
        posDiag = set()
        negDiag = set()

        res = []
        board = [["."] * n for i in range(n)]

        def backtrack(r):
            if r == n:
                copy = ["".join(row) for row in board]
                res.append(copy)
                return

            for c in range(n):
                if c in col or (r + c) in posDiag or (r - c) in negDiag:
                    continue

                col.add(c)
                posDiag.add(r + c)
                negDiag.add(r - c)
                board[r][c] = "Q"

                backtrack(r + 1)

                col.remove(c)
                posDiag.remove(r + c)
                negDiag.remove(r - c)
                board[r][c] = "."

        backtrack(0)
        return res

JavaScript

class Solution {
    /**
     * @param {number} n
     * @return {string[][]}
     */
    solveNQueens(n) {
        const col = new Set();
        const posDiag = new Set();
        const negDiag = new Set();

        const res = [];
        const board = Array.from({ length: n }, 
                      () => Array(n).fill('.'));

        /**
         * @param {number} r
         * @return {void}
         */
        function backtrack(r) {
            if (r === n) {
                res.push(board.map(row => row.join('')));
                return;
            }

            for (let c = 0; c < n; c++) {
                if (col.has(c) || posDiag.has(r + c) ||
                    negDiag.has(r - c)) {
                    continue;
                }

                col.add(c);
                posDiag.add(r + c);
                negDiag.add(r - c);
                board[r][c] = 'Q';

                backtrack(r + 1);

                col.delete(c);
                posDiag.delete(r + c);
                negDiag.delete(r - c);
                board[r][c] = '.';
            }
        }

        backtrack(0);
        return res;
    }
}

Question 4: Partition Equal Subset Sum

Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.

Example 1:

Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.

Constraints :

1 <= nums.length <= 200
1 <= nums[i] <= 100

Code:

C++

Java

Python

C++

class Solution {
public:
    bool canPartition(vector< int>& nums) {
        int sum = 0;
        for (int num : nums)
            sum += num;
        if (sum % 2 != 0)
            return false;
        int req = sum / 2;
        int n = nums.size();
        vector< bool> dp(req + 1, false);
        dp[0] = true;
        for (int i = 0; i < n; i++) {
            for (int j = req; j >= nums[i]; j--) {
                dp[j] = dp[j] || dp[j - nums[i]];
            }
        }
        return dp[req];
    }
};

Java

class Solution {
    public boolean canPartition(int[] nums) {
        int sum=0;
        for(int i:nums)sum+=i;
        if(sum%2!=0)return false;
        int req=sum/2;
        int n=nums.length;
        boolean[] dp=new boolean[req+1];
        dp[0]=true;
        for(int i=0;i=nums[i];j--){
                dp[j]=dp[j] || dp[j-nums[i]];
            }
        }
        return dp[req];
    }
}

Python

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        total_sum = sum(nums)
        if total_sum % 2 != 0:
            return False
        req = total_sum // 2
        n = len(nums)
        dp = [False] * (req + 1)
        dp[0] = True
        for i in range(n):
            for j in range(req, nums[i] - 1, -1):
                dp[j] = dp[j] or dp[j - nums[i]]
        return dp[req]

Question 5: Coin Change II: Counting Distinct Combinations

This problem involves finding the number of distinct combinations of coins that sum up to a given target amount.
It is a classic example of a Dynamic Programming (DP) problem, focusing on combinations rather than permutations.

Problem Description : Coin Change 2

You are given:

An integer array coins where each element represents the denomination of a coin (e.g., 1, 5, 10, etc.).
An integer amount representing the target sum.

Objective: Return the number of distinct combinations of coins that sum up to amount. If it’s impossible to reach the amount, return 0.

Problem Breakdown

Input: 2D grid of non-negative integers.
Objective: Find the length of the longest strictly increasing path.
Movement: Can move to adjacent cells (up, down, left, right) but not diagonally.
Constraints: Each move must go to a cell with a strictly greater value.
Goal: Determine the longest path by efficiently exploring the grid.

Example:

Input: amount = 7, coins = [2,4]

Output: 0

Constraints:

1 <= coins[i] <= 1000
1 <= coins.length <= 100
0 <= amount <= 1000

Code:

Python

Java

C++

JavaScript

Python

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        ROWS, COLS = len(matrix), len(matrix[0])
        dp = {}  # (r, c) -> LIP

        def dfs(r, c, prevVal):
            if (r < 0 or r == ROWS or c < 0 or 
                c == COLS or matrix[r][c] <= prevVal
            ):
                return 0
            if (r, c) in dp:
                return dp[(r, c)]

            res = 1
            res = max(res, 1 + dfs(r + 1, c, matrix[r][c]))
            res = max(res, 1 + dfs(r - 1, c, matrix[r][c]))
            res = max(res, 1 + dfs(r, c + 1, matrix[r][c]))
            res = max(res, 1 + dfs(r, c - 1, matrix[r][c]))
            dp[(r, c)] = res
            return res

        for r in range(ROWS):
            for c in range(COLS):
                dfs(r, c, -1)
        return max(dp.values())

Java

public class Solution {
    public int change(int amount, int[] coins) {
        Arrays.sort(coins);
        int[][] memo = new int[coins.length + 1][amount + 1];
        for (int[] row : memo) {
            Arrays.fill(row, -1);
        }

        return dfs(0, amount, coins, memo);
    }

    private int dfs(int i, int a, int[] coins, int[][] memo) {
        if (a == 0) return 1;
        if (i >= coins.length) return 0;
        if (memo[i][a] != -1) return memo[i][a];

        int res = 0;
        if (a >= coins[i]) {
            res = dfs(i + 1, a, coins, memo);
            res += dfs(i, a - coins[i], coins, memo);
        }
        memo[i][a] = res;
        return res;
    }
}

C++

class Solution {
public:
    int change(int amount, vector& coins) {
        sort(coins.begin(), coins.end());
        vector> memo(coins.size() + 1, 
                            vector(amount + 1, -1));

        return dfs(0, amount, coins, memo);
    }

    int dfs(int i, int a, vector& coins, vector>& memo) {
        if (a == 0) return 1;
        if (i >= coins.size()) return 0;
        if (memo[i][a] != -1) return memo[i][a];

        int res = 0;
        if (a >= coins[i]) {
            res = dfs(i + 1, a, coins, memo);
            res += dfs(i, a - coins[i], coins, memo);
        }
        memo[i][a] = res;
        return res;
    }
};

JavaScript

class Solution {
    /**
     * @param {number} amount
     * @param {number[]} coins
     * @return {number}
     */
    change(amount, coins) {
        coins.sort((a, b) => a - b);
        let memo = Array.from({ length: coins.length + 1 }, () =>
                   Array(amount + 1).fill(-1));

        const dfs = (i, a) => {
            if (a === 0) return 1;
            if (i >= coins.length) return 0;
            if (memo[i][a] !== -1) return memo[i][a];

            let res = 0;
            if (a >= coins[i]) {
                res = dfs(i + 1, a);
                res += dfs(i, a - coins[i]);
            }
            memo[i][a] = res;
            return res;
        };

        return dfs(0, amount);
    }
}

These were some of most Important Uber Coding Questions and Answers. If you want to practice more you can visit our coding blogs to explore more….and also visit PrepInsta Prime Course.

Faq's Related to Uber Hiring Process

Question 1. What types of coding questions are asked in the Uber hiring process?

Answer:

Uber Coding Questions mainly includes topics like arrays, strings, dynamic programming, graphs, and recursion.

Question 2. Which programming languages are allowed for the Uber coding test?

Answer:

Uber allows candidates to code in multiple languages, mainly including C++, Java and Python.

Question 3. How can I prepare for Uber coding round?

Answer:

To prepare effectively:

Practice Coding Questions from our PrepInsta’s Coding Dashboard.
Focus on Time & Space Complexity Efficient solution for the DSA Problem.

Unlock this article for Free,
by logging in

Uber Coding Questions and Answers

Uber Coding Questions with Solutions

Uber SDE 1 Profile Details

Sample Uber Coding Questions with Solutions

Question 1: Finding Longest Repeating Character Replacement Problem

Code

Question 2: Serializing and Deserializing Binary Tree.

Code

Question 3: N Queen Problem

Code

Question 4: Partition Equal Subset Sum

Example 1:

Constraints :

Code:

Question 5: Coin Change II: Counting Distinct Combinations

Constraints:

Code:

Faq's Related to Uber Hiring Process

Question 1. What types of coding questions are asked in the Uber hiring process?

Question 2. Which programming languages are allowed for the Uber coding test?

Question 3. How can I prepare for Uber coding round?

30+ Companies are Hiring

Unlock this article for Free, by logging in

Uber Coding Questions and Answers

Uber Coding Questions with Solutions

Uber SDE 1 Profile Details

Sample Uber Coding Questions with Solutions

Question 1: Finding Longest Repeating Character Replacement Problem

Code

Question 2: Serializing and Deserializing Binary Tree.

Code

Question 3: N Queen Problem

Code

Question 4: Partition Equal Subset Sum

Example 1:

Constraints :

Code:

Question 5: Coin Change II: Counting Distinct Combinations

Constraints:

Code:

Faq's Related to Uber Hiring Process

Question 1. What types of coding questions are asked in the Uber hiring process?

Question 2. Which programming languages are allowed for the Uber coding test?

Question 3. How can I prepare for Uber coding round?

30+ Companies are Hiring

Unlock this article for Free,
by logging in