Cheapest Flights Within K Stops

January 10, 2025

Cheapest Flights Within K Stops

You are given n airports, labeled from 0 to n-1, connected by flights.

Array “flights” contains details of one-way flights in the form [from_i, to_i, price_i], where “from_i” is the starting airport, “to_i” is the destination airport, and “price_i” is the cost of the flight.

There are no duplicate flights, and no flights go from an airport to itself.

You are given three integers:
src: The starting airport.
dst: The destination airport.
k: The maximum number of stops allowed (excluding the source and destination).
The task is to find the cheapest price to travel from src to dst with at most k stops.
If no such route exists, return -1.

Examples related to Cheapest Flights Within K Stops Problem

Example 1:

Explanation: Input: n = 4, flights = [[0,1,200],[1,2,100],[1,3,300],[2,3,100]], src = 0, dst = 3, k = 1
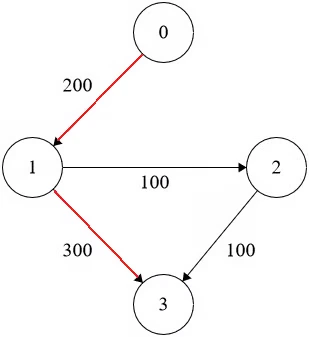
Output: 500
Explanation:
Optimal path with at most 1 stop from airport 0 to 3 is shown in red, with total cost 200 + 300 = 500.
Note that the path [0 -> 1 -> 2 -> 3] costs only 400, and thus is cheaper, but it requires 2 stops, which is more than k.

Example 2:

Input: n = 3, flights = [[1,0,100],[1,2,200],[0,2,100]], src = 1, dst = 2, k = 1
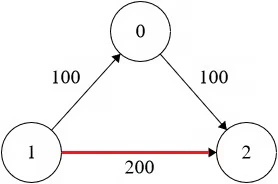
Output: 200
Explanation:
Optimal path with at most 1 stop from airport 1 to 2 is shown in red and has cost 200.

Constraints:

1 <= n <= 100
fromi != toi
1 <= pricei <= 1000
0 <= src, dst, k < n

Hints to solve Cheapest Flights Within K Stops Problem

Recommended Time & Space Complexity

Aim for a solution with O(n + (m * k)) time and O(n) space, where n is the number of cities, m is the number of flights, and k is the maximum number of stops.

Hint 1:

Treat this as a graph problem, where cities are nodes and flights are directed edges with ticket costs as weights.
Can you think of a shortest path algorithm that accommodates the k stops condition? More suitable algorithm than Dijkstra’s may help.

Hint 2:

Consider using the Bellman-Ford algorithm. Initialize a price array of size n with infinity, setting prices[source] = 0.
This array tracks the minimum cost to reach each city. Iterate (k+1) times, updating the cost of each city by extending paths from cities with valid costs.
How would you implement this?

Hint 3:

At each iteration, update the price array with minimum costs by processing each flight.
Use a temporary array to store the updated values.
After completing all iterations, return prices[dst]. If it’s still infinity, return -1.

Methods to Solve Cheapest Flights Within K Stops Problem

There are mainly 3 approaches to solve Cheapest Flights Within K Stops problem:

Dijkstra’s Algorithm
Bellman Ford Algorithm
Shortest Path Faster Algorithm

1. Dijkstra’s Algorithm Method

This is a greedy algorithm used to find the shortest path between a source node and all other nodes in a weighted graph.

It works by selecting the node with the smallest tentative distance, then updating the distances of its neighboring nodes, and repeats this until all nodes are visited.

Time complexity: O((n+m)∗k)
Space complexity: O(n∗k)

Where n is the number of cities, m is the number of flights and k is the number of stops.

C++

Java

Python

JavaScript

C++

class Solution {
public:
    int findCheapestPrice(int n, vector>& flights, int src, int dst, int k) {
        int INF = 1e9;
        vector>> adj(n);
        vector> dist(n, vector(k + 5, INF));
        
        for (auto& flight : flights) {
            adj[flight[0]].emplace_back(flight[1], flight[2]);
        }
        
        dist[src][0] = 0;
        priority_queue, 
                       vector>, greater<>> minHeap;
        minHeap.emplace(0, src, -1);
        
        while (!minHeap.empty()) {
            auto [cst, node, stops] = minHeap.top();
            minHeap.pop();
            if (node == dst) return cst;
            if (stops == k || dist[node][stops + 1] < cst) continue;
            for (auto& [nei, w] : adj[node]) {
                int nextCst = cst + w;
                int nextStops = stops + 1;
                if (dist[nei][nextStops + 1] > nextCst) {
                    dist[nei][nextStops + 1] = nextCst;
                    minHeap.emplace(nextCst, nei, nextStops);
                }
            }
        }
        return -1;
    }
};

Java

public class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int INF = Integer.MAX_VALUE;
        List[] adj = new ArrayList[n];
        int[][] dist = new int[n][k + 5];
        for (int i = 0; i < n; i++) Arrays.fill(dist[i], INF);
        
        for (int i = 0; i < n; i++) adj[i] = new ArrayList<>();
        for (int[] flight : flights) {
            adj[flight[0]].add(new int[]{flight[1], flight[2]});
        }
        
        dist[src][0] = 0;
        PriorityQueue minHeap = new PriorityQueue<>(
            Comparator.comparingInt(a -> a[0])
        );
        minHeap.offer(new int[]{0, src, -1});

        while (!minHeap.isEmpty()) {
            int[] top = minHeap.poll();
            int cst = top[0], node = top[1], stops = top[2];
            if (node == dst) return cst;
            if (stops == k || dist[node][stops + 1] < cst) continue;
            for (int[] neighbor : adj[node]) {
                int nei = neighbor[0], w = neighbor[1];
                int nextCst = cst + w;
                int nextStops = stops + 1;
                if (dist[nei][nextStops + 1] > nextCst) {
                    dist[nei][nextStops + 1] = nextCst;
                    minHeap.offer(new int[]{nextCst, nei, nextStops});
                }
            }
        }
        return -1;
    }
}

Python

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        INF = float("inf")
        adj = [[] for _ in range(n)]
        dist = [[INF] * (k + 5) for _ in range(n)]
        for u, v, cst in flights:
            adj[u].append([v, cst])
        
        dist[src][0] = 0
        minHeap = [(0, src, -1)] # cost, node, stops
        while len(minHeap):
            cst, node, stops = heapq.heappop(minHeap)
            if dst == node: return cst
            if stops == k or dist[node][stops + 1] < cst:
                continue
            for nei, w in adj[node]:
                nextCst = cst + w
                nextStops = 1 + stops
                if dist[nei][nextStops + 1] > nextCst:
                    dist[nei][nextStops + 1] = nextCst
                    heapq.heappush(minHeap, (nextCst, nei, nextStops))

        return -1

JavaScript

class Solution {
    /**
     * @param {number} n
     * @param {number[][]} flights
     * @param {number} src
     * @param {number} dst
     * @param {number} k
     * @return {number}
     */
    findCheapestPrice(n, flights, src, dst, k) {
        const INF = Infinity;
        const adj = Array.from({ length: n }, () => []);
        const dist = Array.from({ length: n }, () => 
                     Array(k + 5).fill(INF));
        
        for (let [u, v, cst] of flights) {
            adj[u].push([v, cst]);
        }
        
        dist[src][0] = 0;
        const minHeap = new MinPriorityQueue(entry => entry[0]); 
        minHeap.push([0, src, -1]); // cost, node, stops
        while (!minHeap.isEmpty()) {
            const [cst, node, stops] = minHeap.pop();
            if (node === dst) return cst;
            if (stops === k || dist[node][stops + 1] < cst) continue;
            for (let [nei, w] of adj[node]) {
                const nextCst = cst + w;
                const nextStops = stops + 1;
                if (dist[nei][nextStops + 1] > nextCst) {
                    dist[nei][nextStops + 1] = nextCst;
                    minHeap.push([nextCst, nei, nextStops]);
                }
            }
        }
        return -1;
    }
}

2. Bellman Ford Algorithm

Dynamic programming approach that calculates the shortest path in a weighted graph, even when negative edge weights exist. It works by iteratively relaxing all edges, updating the shortest distance for each node, and can detect negative weight cycles.

Time complexity: O(n+(m∗k))
Space complexity: O(n)

Where n is the number of cities, m is the number of flights and k is the number of stops.

Code:

C++

Java

Python

JavaScript

C++

class Solution {
public:
    int findCheapestPrice(int n, vector>& flights, int src, int dst, int k) {
        vector prices(n, INT_MAX);
        prices[src] = 0;

        for (int i = 0; i <= k; i++) {
            vector tmpPrices = prices;

            for (const auto& flight : flights) {
                int s = flight[0];
                int d = flight[1];
                int p = flight[2];

                if (prices[s] == INT_MAX)
                    continue;

                if (prices[s] + p < tmpPrices[d])
                    tmpPrices[d] = prices[s] + p;
            }

            prices = tmpPrices;
        }

        return prices[dst] == INT_MAX ? -1 : prices[dst];
    }
};

Java

public class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int[] prices = new int[n];
        Arrays.fill(prices, Integer.MAX_VALUE);
        prices[src] = 0;

        for (int i = 0; i <= k; i++) {
            int[] tmpPrices = Arrays.copyOf(prices, n);

            for (int[] flight : flights) {
                int s = flight[0];
                int d = flight[1];
                int p = flight[2];

                if (prices[s] == Integer.MAX_VALUE) {
                    continue;
                }

                if (prices[s] + p < tmpPrices[d]) {
                    tmpPrices[d] = prices[s] + p;
                }
            }

            prices = tmpPrices;
        }

        return prices[dst] == Integer.MAX_VALUE ? -1 : prices[dst];
    }
}

Python

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        prices = [float("inf")] * n
        prices[src] = 0

        for i in range(k + 1):
            tmpPrices = prices.copy()

            for s, d, p in flights:  # s=source, d=dest, p=price
                if prices[s] == float("inf"):
                    continue
                if prices[s] + p < tmpPrices[d]:
                    tmpPrices[d] = prices[s] + p
            prices = tmpPrices
        return -1 if prices[dst] == float("inf") else prices[dst]

JavaScript

class Solution {
    /**
     * @param {number} n
     * @param {number[][]} flights
     * @param {number} src
     * @param {number} dst
     * @param {number} k
     * @return {number}
     */
    findCheapestPrice(n, flights, src, dst, k) {
        let prices = new Array(n).fill(Number.MAX_SAFE_INTEGER);
        prices[src] = 0;

        for (let i = 0; i <= k; i++) {
            const tmpPrices = [...prices];

            for (const flight of flights) {
                const s = flight[0];
                const d = flight[1];
                const p = flight[2];

                if (prices[s] === Number.MAX_SAFE_INTEGER) continue;

                if (prices[s] + p < tmpPrices[d]) tmpPrices[d] = prices[s] + p;
            }

            prices = tmpPrices;
        }

        return prices[dst] === Number.MAX_SAFE_INTEGER ? -1 : prices[dst];
    }
}

3. Shortest Path Faster Algorithm

This is an optimized version of the Bellman-Ford algorithm, where nodes are processed in order of the shortest known distance. It uses a priority queue to speed up the relaxation process, offering better performance for many graphs.

Time complexity: O(n∗k)
Space complexity: O(n+m)

Where n is the number of cities, m is the number of flights and k is the number of stops.

Code:

C++

Java

Python

JavaScript

C++

class Solution {
public:
    int findCheapestPrice(int n, vector>& flights, int src, int dst, int k) {
        vector prices(n, INT_MAX);
        prices[src] = 0;
        vector>> adj(n);
        for (const auto& flight : flights) {
            adj[flight[0]].emplace_back(flight[1], flight[2]);
        }

        queue> q;
        q.push({0, src, 0});

        while (!q.empty()) {
            auto [cst, node, stops] = q.front();
            q.pop();
            if (stops > k) continue;

            for (const auto& neighbor : adj[node]) {
                int nei = neighbor.first, w = neighbor.second;
                int nextCost = cst + w;
                if (nextCost < prices[nei]) {
                    prices[nei] = nextCost;
                    q.push({nextCost, nei, stops + 1});
                }
            }
        }
        return prices[dst] == INT_MAX ? -1 : prices[dst];
    }
};

Java

public class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        int[] prices = new int[n];
        Arrays.fill(prices, Integer.MAX_VALUE);
        prices[src] = 0;
        List[] adj = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<>();
        }
        for (var flight : flights) {
            adj[flight[0]].add(new int[] { flight[1], flight[2] });
        }

        Queue q = new LinkedList<>();
        q.offer(new int[] { 0, src, 0 });

        while (!q.isEmpty()) {
            var curr = q.poll();
            int cst = curr[0], node = curr[1], stops = curr[2];
            if (stops > k) continue;

            for (var neighbor : adj[node]) {
                int nei = neighbor[0], w = neighbor[1];
                int nextCost = cst + w;
                if (nextCost < prices[nei]) {
                    prices[nei] = nextCost;
                    q.offer(new int[] { nextCost, nei, stops + 1 });
                }
            }
        }
        return prices[dst] == Integer.MAX_VALUE ? -1 : prices[dst];
    }
}

Python

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        prices = [float("inf")] * n
        prices[src] = 0
        adj = [[] for _ in range(n)]
        for u, v, cst in flights:
            adj[u].append([v, cst])

        q = deque([(0, src, 0)])
        while q:
            cst, node, stops = q.popleft()
            if stops > k:
                continue
            
            for nei, w in adj[node]:
                nextCost = cst + w
                if nextCost < prices[nei]:
                    prices[nei] = nextCost
                    q.append((nextCost, nei, stops + 1))

        return prices[dst] if prices[dst] != float("inf") else -1

JavaScript

class Solution {
    /**
     * @param {number} n
     * @param {number[][]} flights
     * @param {number} src
     * @param {number} dst
     * @param {number} k
     * @return {number}
     */
    findCheapestPrice(n, flights, src, dst, k) {
        const prices = Array(n).fill(Infinity);
        prices[src] = 0;
        const adj = Array.from({ length: n }, () => []);
        
        for (const [u, v, cst] of flights) {
            adj[u].push([v, cst]);
        }

        const q = new Queue([[0, src, 0]]); // [cost, node, stops]

        while (!q.isEmpty()) {
            const [cst, node, stops] = q.pop();
            if (stops > k) continue;

            for (const [nei, w] of adj[node]) {
                const nextCost = cst + w;
                if (nextCost < prices[nei]) {
                    prices[nei] = nextCost;
                    q.push([nextCost, nei, stops + 1]);
                }
            }
        }
        return prices[dst] === Infinity ? -1 : prices[dst];
    }
}

Unlock this article for Free,
by logging in

Cheapest Flights Within K Stops