Recursion in Python Language
What is Recursion?
Recursion in Python Language is a method of solving a problem where the solution depends on solutions to smaller instances of the same problem. Such problems can generally be solved by iteration, but this needs to identify and index the smaller instances at programming time. We’ll discuss recursion in depth as we go.
Recursion in Python
Recursion in computer science, is basically calling out the function from the function itself. For instance,
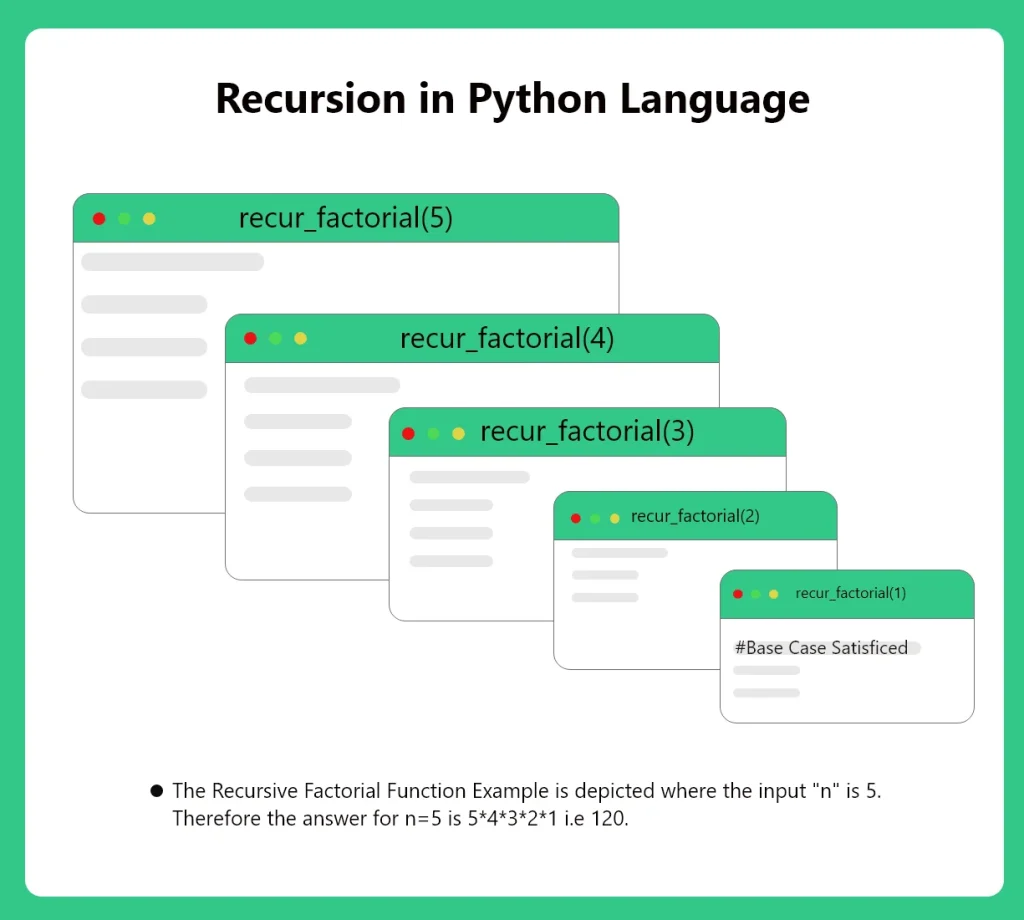
def recur_factorial(n):
if n == 1:
return n
else:
return n*recur_factorial(n-1)
The above code is for performing factorial operation on a given number using recursion. Here we can see that the function recur_factorail() is taking a parameter “n” and later been called within itself. Such functions which are called within themselves are called recursive functions. The objective of recursion is to break down the problem into multiple tiny proportions but with same function structure.
We’ll discuss more about recursion and recursive functions on this page in the sections below.
What is the need for Recursion?
Even though the recursive function take more time to compile, people prefer using recursion over loop iterations. Recursion is made for solving problems that can be broken down into smaller, repetitive problems. It is especially good for working on things that have many possible branches and are too complex for an iterative approach. Recursive thinking is really important in programming. Often, the recursive solution can be simpler to read than the iterative one. Some problems such as parsing a tree or performing tree operations or graphs operations can easily done with minimal amount of code. Here are a few points highlighting the importance of recursion,
- Improves Readability of Complex codes.
- Minimal Effort while writing the code.
- Used for Solving and operating on complex data structure such as trees and graphs.
- Enables easy debugging of the code.
But as every loop has a terminating statement or a condition to check for termination, Recursive function also has a base condition for termination. We’ll discuss about the components of a recursive function in detail in the next section.
Components of a Recursive Function
Just like every loop has three sections, The Condition, Operation and Incrementation, a Recursive function can also be summed up as three components.
- Base Case
- Recursive Step Call
- Function Body
Let’s discuss these three components using the above Factorial code in detail.
# Recursive Factorial Function
def recur_factorial(n):
# Function Body
print("iteration at {}".format(n))
# Base Case
if n == 1:
return n
# Recursive Step Call
else:
return n*recur_factorial(n-1)
1. Base Case
As loops in programming languages have a terminating statement to avoid infinite iteration of a loop, the Recursive functions have a Base case. Base Case is a condition that is checked every time a Recursive function is called. Let’s try and understand using the factorial example,
if n == 1: return n
The above code snippet is the base case for the factorial recursive function. It checks whether the value of the parameter passed is 1. If true it returns 1 termination the recursive sequence.
2. Recursive Step Call
As loops in programming languages have iterator variables that are incremented to iterate through the container values, Recursive functions have a Recursive Step Call. It’s basically a function call but the parameter is decremented by 1. This call acts as a stepdown for the recursive function. All these Recursive Step Call can be visualized in the form of a recursion tree. Let’s try and understand using the factorial example,
else: return n*recur_factorial(n-1)
Here in the above code snippet, the function recur_factorial() is called within itself while decrementing the parameter value “n”. The value returned by all the recursion calls that’ll be triggered will return some values which will be multiplied by “n”. for instance the final returned value for n = 2 will be 2*1 which is equal to 2!.
3. Function Body
Just as a loop in programming languages have a body where all the operations are done, Recursive functions have a body as well. The body of the recursive factorial function is as follows,
print("iteration at {}".format(n))This statement prints the iteration the recursive function is currently at.
All these Components together form structure for all the recursive functions.
Most Common Recursion mistakes
The downside is that they can cause infinite loops and other unexpected results if not written properly. For example, in the example above, the function is terminated if the number is 0 or less or greater than 9. If proper cases are not included in a recursive function to stop the execution, it will repeat forever, causing the program to crash or become unresponsive.
Here are some of the most common challenges faced by programmers while write a recursive code,
- Program does not terminate
- Make sure the problem size decreases and there is a correct base case
- Slow performance due to excessive re-computations
Pitfalls or Disadvantages of Recursion
Recursion, although being a very powerful algorithm, has it’s own set of drawbacks. Below mentioned are some of the drawbacks of recursion,
- Hard to comprehend, difficult concept.
- Slower execution than iterative algorithms.
- Recursive code takes up more space ruining the space complexity of the code.
Login/Signup to comment