Quick Sort in Python
Introduction to Quick Sort in Python
Quick sort in Python is a widely used sorting algorithm that follows the divide-and-conquer strategy to sort an array or list. and Quick Sort stands out for its remarkable speed and effectiveness.
In this guide, we will delve deep into the inner workings of Quick Sort, provide Python code examples for its implementation, explore its time and space complexity, and offer insights into when and why Quick Sort is a preferred choice for sorting large datasets.
What is Quick Sort in Python?
Quick Sort is known as a “divide and conquer” algorithm because it employs a recursive approach that breaks a problem into smaller subproblems, solves each subproblem independently, and then combines the solutions of the subproblems to obtain the final solution.
Working of Quick Sort in Python
Certainly, here’s a concise explanation of how Quick Sort works in five key points:
Pivot Selection: Quick Sort begins by selecting a pivot element from the array. The choice of pivot can vary but often involves selecting the middle element for simplicity.
Partitioning: The array is then partitioned so that elements smaller than the pivot are on the left, and elements greater than the pivot are on the right. The pivot itself is now in its final sorted position.
Recursive Sorting: Quick Sort is applied recursively to the left and right subarrays created during partitioning. This recursive process continues until all subarrays are sorted.
Combining Results: As recursion unwinds, the sorted subarrays are combined with the pivot to create the fully sorted array.
Base Case: The recursion stops when subarrays have one element or are empty, as they are considered sorted at this point. This divide-and-conquer approach efficiently sorts the entire array.
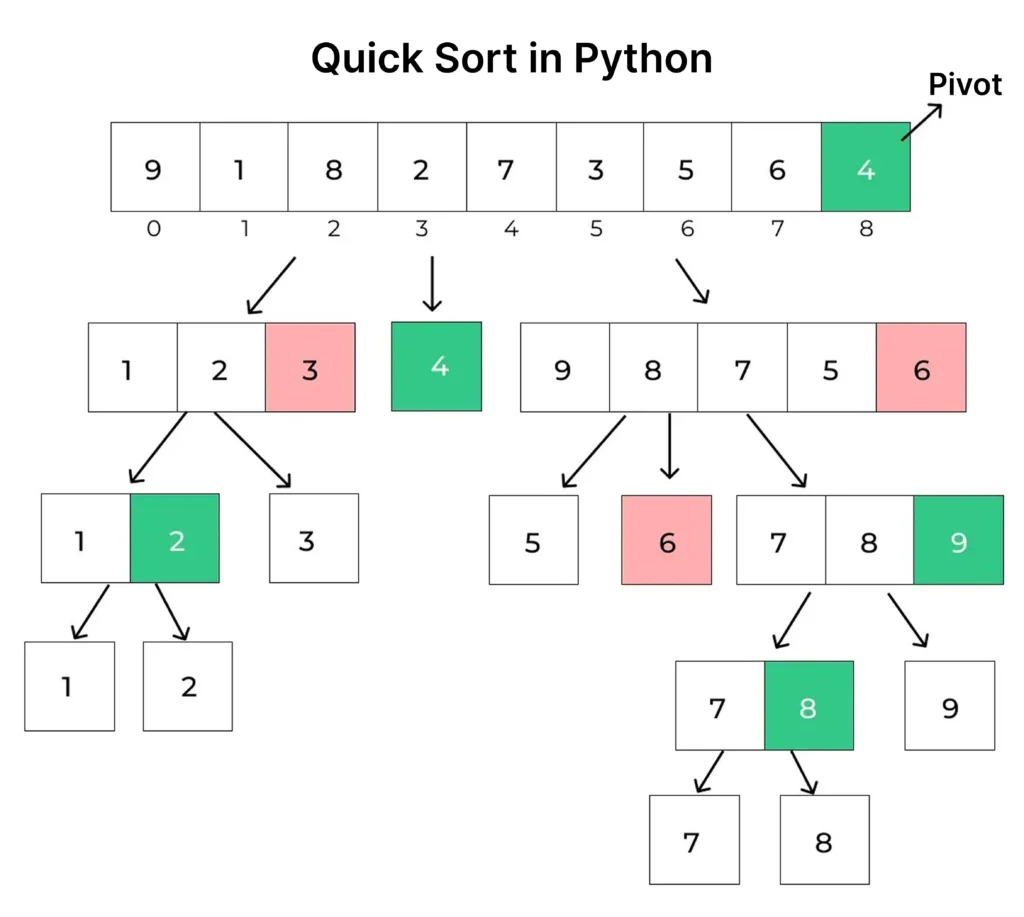
Algorithm for Quick Sort in Python
Algorithm describes the steps for performing Quick Sort in Python:
This algorithm follows these steps:
Choose a Pivot: Select a pivot element from the array. In this example, we choose the middle element.
Partition the Array: Divide the array into three subarrays: one for elements less than the pivot, one for elements equal to the pivot, and one for elements greater than the pivot.
Recursively Sort: Apply the Quick Sort algorithm recursively to the left and right subarrays, which are the ones containing elements less than and greater than the pivot.
Combine Results: Combine the sorted left subarray, the pivot (which is now in its correct position), and the sorted right subarray to obtain the final sorted array.
Implementation of Quick Sort in Python
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2] # Choose a pivot element (in this case, the middle element)
left = [x for x in arr if x < pivot] # Elements less than the pivot middle = [x for x in arr if x == pivot] # Elements equal to the pivot right = [x for x in arr if x > pivot] # Elements greater than the pivot
# Recursively sort the left and right partitions
return quick_sort(left) + middle + quick_sort(right)
# Example usage:
my_list = [3, 6, 8, 10, 1, 2, 1]
sorted_list = quick_sort(my_list)
print(sorted_list)
Output :
Original list: [3, 6, 8, 10, 1, 2, 1] Sorted list: [1, 1, 2, 3, 6, 8, 10]
Explanation
The Python code implements the Quick Sort algorithm. It recursively divides an input list into smaller sublists by selecting a pivot element (usually the middle).
- Elements are then partitioned into three sublists: those less than the pivot, equal to the pivot, and greater than the pivot.
- The algorithm continues to recursively sort the left and right sublists until the base case is reached (lists with one or zero elements). Finally, it combines the sorted sublists and the pivot to produce a fully sorted list.
Time and Space Complexity for Insertion Sort in Python
Quick Sort in Python has the following time and space complexity:
Time Complexity (Average Case):
- O(n log n)
- Quick Sort has an average-case time complexity of O(n log n), where “n” is the number of elements in the list. This makes it highly efficient for large datasets.
Time Complexity (Worst Case):
- O(n^2)
- In the worst-case scenario (e.g., when the pivot is consistently chosen poorly), Quick Sort can degrade to O(n^2), which is less efficient. However, this is rare in practice and can be mitigated with proper pivot selection strategies.
Space Complexity:
- O(log n) on average
- Quick Sort typically has a space complexity of O(log n) because it uses recursion and only requires a small amount of additional memory for the call stack. However, in the worst case, it can require O(n) additional memory for the stack due to unbalanced partitioning.
To wrap it up:
In this exploration of Quick Sort in Python, we’ve delved into a powerful and efficient sorting algorithm. Quick Sort, known for its average-case time complexity of O(n log n), excels in sorting large datasets swiftly. It achieves this by cleverly partitioning the array, dividing and conquering until the elements are in their rightful order.
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Question 1.
How is the pivot element chosen?
The choice of the pivot element can impact Quick Sort’s performance. Common strategies include selecting the middle element, the first element, or using a randomized approach to ensure balanced partitions.
Question 2.
What are the advantages of Quick Sort?
Quick Sort is known for its speed and efficiency, especially for large datasets. It’s an in-place sorting algorithm, meaning it doesn’t require additional memory, and it’s often faster than other popular sorting algorithms like Merge Sort or Bubble Sort.
Question 3.
How does Quick Sort compare to other sorting algorithms?
Quick Sort often outperforms other sorting algorithms like Bubble Sort and Insertion Sort, especially for larger datasets. It’s on par with Merge Sort but is often preferred due to its in-place sorting capability.
Question 4.
Are there any limitations or drawbacks to Quick Sort?
Quick Sort’s main limitation is its potential worst-case time complexity of O(n^2). It can also require more memory than some other algorithms due to its recursive nature.
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Login/Signup to comment