Traversal in Trees

August 22, 2019

Traversal

  1. The term traversal means to visit each node in a tree exactly once. In linear lists the order of traversal is vividly first to last. However, in trees there exists no such natural linear order. 
  2. In binary tree or binary search trees, there exist two methods for traversal, namely:
    • Depth first search.
    • Breadth first search.
introduction

Let us understand the types of traversal with the help of an example

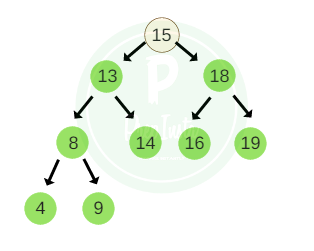
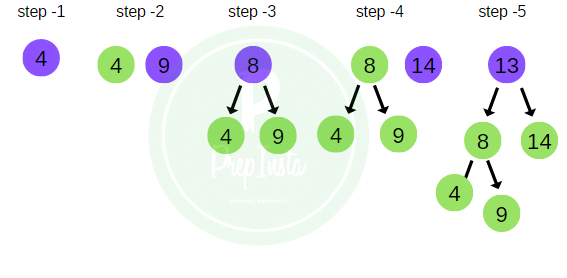
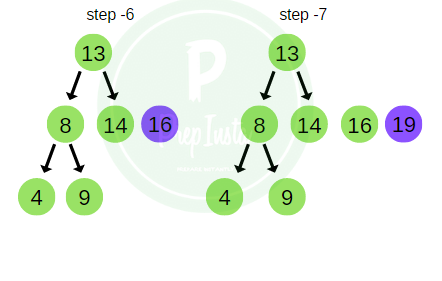
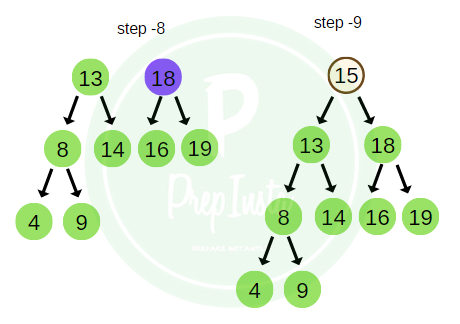
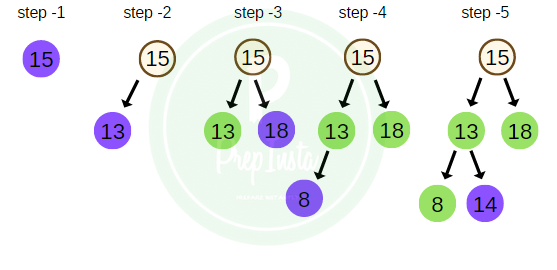
  • The elements of the tree are T = [ 15, 18, 13, 8, 14, 4, 16, 9, 19 ]
  • Using the tree in the image above we will further study how the different methods of traversal of a tree yield different result.
  • This particular tree follows the BST properties for instance, but the case of binary tree will be same as a BST.
example traverse

Types of Traversal

1. Depth first search

  • DFS can be defined as an algorithm, based on backtracking, dedicated to traversing a tree structure by first visiting the root first and then the left sub-tree and the right sub-tree.
  • It is of three types:

    • In-order traversal.

    • Pre-order traversal.

    • Post-order traversal.

  • The functions for traversal via these methods can be kept concise if we understand the recursive nature of the binary tree or binary search trees.
  • If we recall, a binary tree or binary search trees is recursive data structure in which each sub tree is a binary tree or binary search trees itself..
  • Hence the methods of traversal differ in the order in which these three operations are performed.

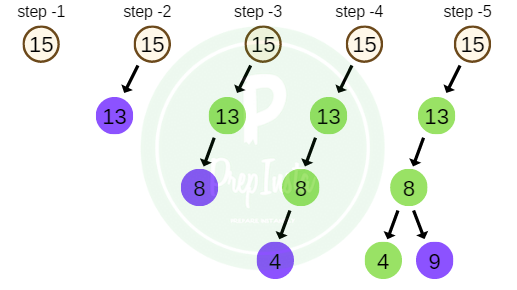
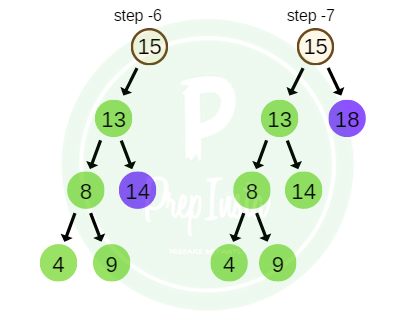
  •  Pre-Order Traversal

    For traversal of a non-empty binary tree or binary search tree in Pre-order, following sequence of operations is performed.

    • Visit the root node.
    • Traverse the left sub tree in pre-order.
    • Traverse the right sub tree in post-order.
 
Considering the tree example above the Pre- order traversal of the tree would be,
 
pre_order = 15 , 13 , 8 , 4 , 9 , 14 , 18 , 16 , 19.
preorder1
preorder2
preorder3

  • In-Order Traversal

    For traversal of a non-empty binary tree or binary search tree in In-order, following sequence of operations is performed.

    • Traverse the left sub tree in in-order.
    • Visit the root node.
    • Traverse the right sub tree in in-order.

 

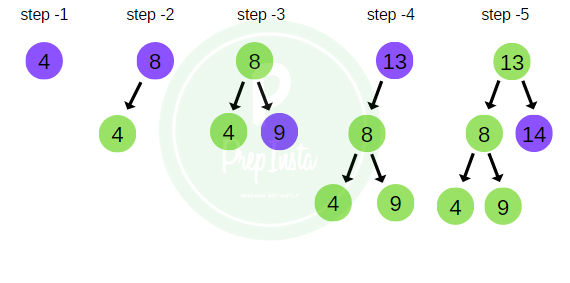
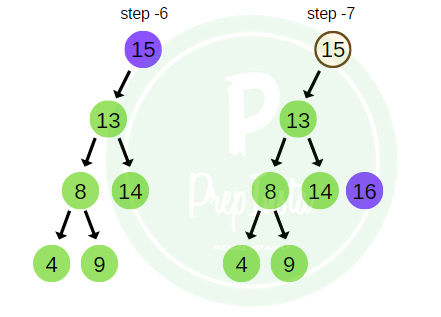
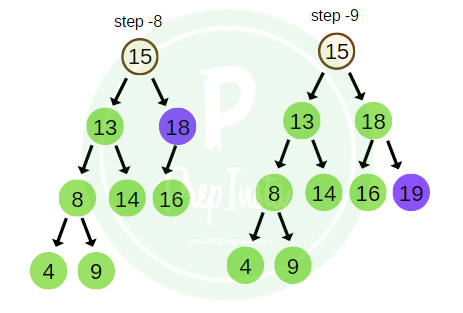
Considering the tree example above the In- order traversal of the tree would be,

in_order = 4 , 8 , 9 , 13 , 14 , 15 , 16 , 18 , 19.

inorder1
inorder2
inorder3

  • Post-Order Traversal

    For traversal of a non-empty binary tree or binary search tree in Post-order, following sequence of operations is performed.

    • Traverse the left sub tree in post-order.
    • Traverse the right sub tree in post-order.
    • Visit the root node.

     

Considering the tree example above the Pre- order traversal of the tree would be,

post_order = 4 , 9 , 8 , 14 , 13 , 16 , 19 , 18 , 15

postorder1
postorder2
postorder3

2. Breadth first search

  • BFS can be defined as an algorithm dedicated to traversing a tree structure, level by level or depth by depth.
  • This category of tree traversal initializes from the root node and explores all the adjacent nodes on a current level and then moves on to the next level, and so on.

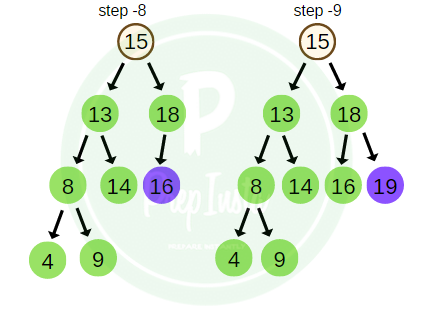
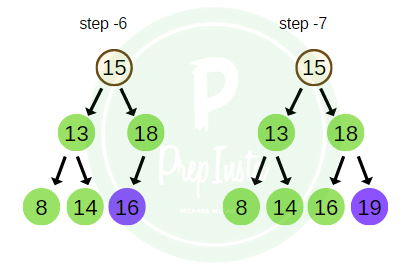
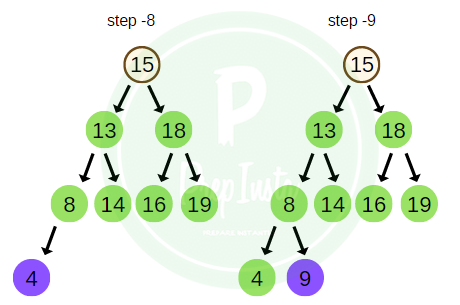
Taking the same example as above, the BFS traversal of the tree is shown in the image here.

bfs_traversal = 15 , 13 , 18 , 8 , 14 , 16 , 19 , 4 , 9

BFS1
BFS2
BFS3

Implementation of Traversal on a Tree.

#include<stdio.h>
#include<stdlib.h>
struct binarySearchTree
{
 int element;
 struct binarySearchTree *left;
 struct binarySearchTree *right;
};
 
struct binarySearchTree *insert(struct binarySearchTree *,int);
void inorder(struct binarySearchTree *);
void postorder(struct binarySearchTree *);
void preorder(struct binarySearchTree *);
struct binarySearchTree *delet(struct binarySearchTree *,int);
struct binarySearchTree *search(struct binarySearchTree *);
 
int main(void)
{
 
 struct binarySearchTree *root;
 int option, item,item_no;
 root = NULL;
 //clrscr();
/* rear  = NULL;*/
 do
 {
  do
  {
   printf("\n\t 1. Enter Element in Tress");
   printf("\n\t 2. Preorder traversal");
   printf("\n\t 3. Inorder traversal");
   printf("\n\t 4. Postorder traversal");
   printf("\n\t 5. Exit ");
   printf("\n\t Enter option : ");
   scanf(" %d",&option);
   if(option<1 || option>5)
      printf("\n Invalid option - try again");
  }while (option<1 || option>5);
  switch(option)
  {
   case 1:
  printf("\n Enter new element: ");
  scanf("%d", &item);
  root= insert(root,item);
  printf("\n root is %d",root->element);
  break;
   case 2:
 printf("\n Preorder traversal of tree is : ");
 preorder(root);
 break;
   case 3:
 printf("\n Inorder traversal of Tree is : ");
 inorder(root);
 break;
   case 4:
 printf("\n Postorder traversal of Tree is : ");
 postorder(root);
 break;
   default:
  printf("\n End of program ");
   } /* end of switch */
  }while(option !=5);
 return(0);
}
 
struct binarySearchTree *insert(struct binarySearchTree *root, int x)
{
 if(!root)
  {
    root=(struct binarySearchTree*)malloc(sizeof(struct binarySearchTree));
    root->element = x;
    root->left = NULL;
    root->right = NULL;
    return(root);
  }
  if(root->element > x)
     root->left = insert(root->left,x);
  else
   {
     if(root->element < x)
root->right = insert(root->right,x);
   }
   return(root);
 }
 
 void inorder(struct binarySearchTree *root)
 {
    if(root != NULL)
   {
     inorder(root->left);
     printf(" %d",root->element);
     inorder(root->right);
   }
   return;
 }
 
 void postorder(struct binarySearchTree *root)
 {
    if(root != NULL)
   {
     postorder(root->left);
     postorder(root->right);
     printf(" %d",root->element);
   }
   return;
 }
 
 void preorder(struct binarySearchTree *root)
 {
    if(root != NULL)
   {
     printf(" %d",root->element);
     preorder(root->left);
     preorder(root->right);
   }
   return;
 }

One comment on “Traversal in Trees”