Searching In A Binary Tree In C++

January 24, 2021

Searching In A Binary Tree

Given a tree and the number, we need to find to check whether the number is present in the binary tree or not. There can be different ways to approach this problem. In this articles, two ways are discussed, level order and recursion.

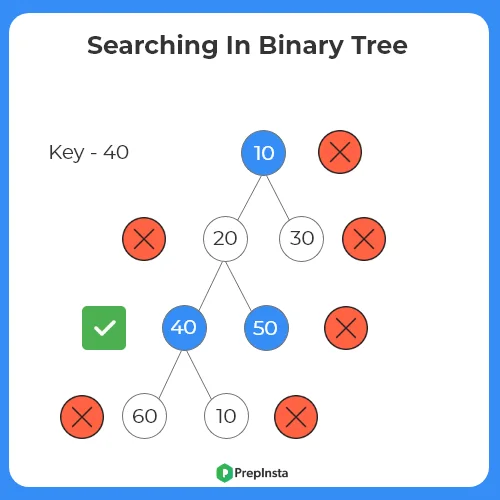
Algorithm Using Level Order Traversal:

  1. Initialize the queue.
  2. Add root to the queue.
  3. Until the queue is empty, add the left child and the right child of the current node.
  4. Pop the node.
  5. Traverse the queue, check whether key is equal to the value of node.
  6. If found return true otherwise false.

 

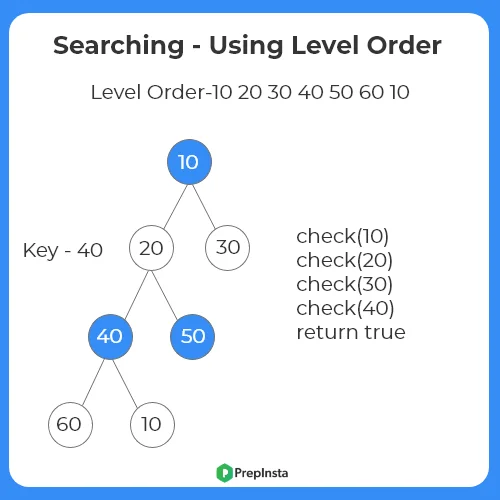
C++ Program To do a level order Search in A Binary Tree
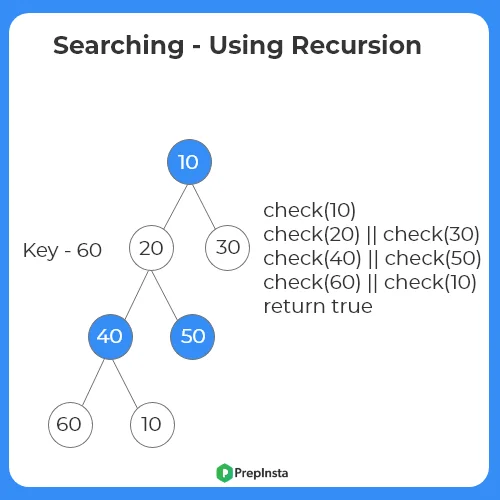
C++ Program To Search in A Binary Tree using recursion

Algorithm Using Recursion:

  1. If root is null, return.
  2. Else Recursively check for the left subtree and the right subtree.
  3. Return true if found.

Code (Level Order):

#include<bits/stdc++.h> 
using namespace std; 
class Tree {
    public:
        int data;
        Tree* left = NULL,*right = NULL;
        // Constructor initialised
        Tree(int x) {
            data = x;
            left = NULL;
            right = NULL;
        }
};
// To check whether equal or not
bool check(int key,int element) {
    if (key == element) return true;
    return false;
}
void level_order(Tree *root, int key) {
    if (root == NULL) return;
    queue q, lev;
    q.push(root);
    // Getting Level Order
    while (!q.empty()) {
        Tree * temp = q.front();
        lev.push(temp);
        // Adding left child
        if (temp -> left != NULL) {
            q.push(temp -> left);
        }
        // Adding Right child
        if (temp -> right != NULL) {
            q.push(temp -> right);
        }
        q.pop();
    }
    bool ok = false;
    while (!lev.empty()) {
        if (check(lev.front() -> data,key)) {
            cout << “Found\n“;
            ok = true;
        }
        lev.pop();
    }
    // If not found
    if (!ok) {
        cout <<“Not Found”;
    }
}
int main() {
    Tree *root = new Tree(10);
    root -> left = new Tree(20);
    root -> right = new Tree(30);
    root -> left -> left = new Tree(40);
    root -> left -> right = new Tree(50);
    level_order(root,40); 
    return 0;
}

Output:

Found
 

Code (Recursion):

#include<bits/stdc++.h> 
using namespace std; 
class Tree {
    public:
        int data;
        Tree* left = NULL,*right = NULL;
        // Constructor initialised
        Tree(int x) {
            data = x;
            left = NULL;
            right = NULL;
        }
};
// To check whether equal or not
bool check_element(Tree * root, int key) {
    // If root is null, element is not found:Backtrack 
    if (root == NULL) {
        return false;
    }
    // Check whether same or not
    if (root -> data == key) {
        return true;
    }
    // Recursively call for left and right subtree
    return (check_element(root -> left, key) || check_element(root -> right, key));
}
int main() {
    Tree *root = new Tree(10);
    root -> left = new Tree(20);
    root -> right = new Tree(30);
    root -> left -> left = new Tree(40);
    root -> left -> right = new Tree(50);
    if (check_element(root,45)) {
        cout << “Found\n“;
    }
    else {
        cout << “Not Found\n“;
    }
    return 0;
}

 

Output:

Not Found

Time Complexity For Searching Element In A Tree

Time Complexity

O(n) Queue and Recursion

Space Complexity

O(1) Queue and Recursion