B- Trees

August 22, 2019

Introduction to B- Trees

A B – Tree can be defined as a multi-way search tree of order m such that it follows the conditions stated:

  • All the internal nodes (except the root node) have at least m/2 children and at most m children.
  • The non – leaf root node may have at most m non empty child and at least two child nodes.
  • In a B- Tree, the root node is the only node that can exist without no child nodes.
  • If a node has m children then it must have (m – 1) values. All these values of a particular node are in increasing order.
  • All the values of a node that appear on the leftmost child of the node are smaller than the first value of that node. Similarly, all the values that appear on the rightmost child of a node are greater than the last value of that node.
  • If a and b are any two ith and (i+1)th values of the node , where x < y, then all the values appearing on the (i+1)th sub tree of the that node are greater than x and less than y. 
  • All the leaf nodes should appear on the same level.
  • The primary goal to use a B-tree is to reduce the number of disk access. Majority of tree operations such as searching, traversal ,insertion, etc, take O(n) time, where n is the height of the tree.
  • A B-Tree of  degree T can have –
    •  T-1 minimum keys.
    • 2T-1 maximum keys.
btree

Operations in a B-Tree

  • Insertion.
  • Deletion

Representation of B- Tree

The structure of a node in B-Tree can be represented as follows:

  • struct btree_node
  • {
  •         int c;
  •         int val[M + 1];
  •         struct btree_node *child[M + 1]
  • };
  1. Here c represents the number of children a particular node can have.
  2. Array val represents the values of the node stored in it.
  3. Array child stores the address of child nodes.
  4. The macro M signifies the maximum number of values a node can hold.
b8

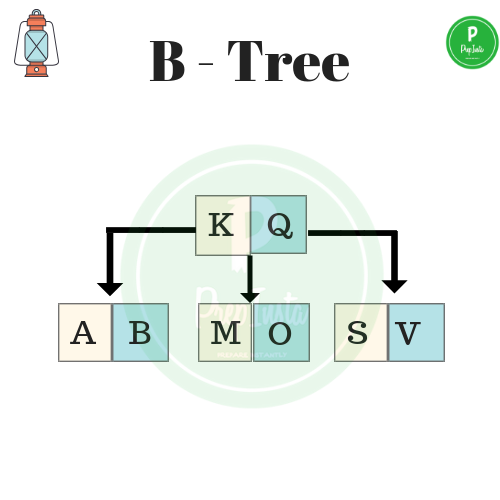
Creation of a B-Tree:

Let us consider a B-Tree of order 5. It means we can have a maximum number of 4 values that any node can hold.

For reference we see the given image. we can see that any node can have at most 4 values. 

But if in any case we are given the degree of a tree; for instance consider t = 2, then,

  • Minimum number of keys that a tree can hold can be calculated as
    • min_key = t – 1=> 2 – 1 => min_key = 1
  • Maximum number of keys that a tree can hold can be calculated as
    • max_key = 2t – 1 => 2(2) – 1 => 4 – 1 => max_key = 3
 
Let us perform a step by step construction of a B-Tree.
Consider we have to construct a B-tree where the elements are given as, 20 , 30 , 35 , 85 , 5 , 10 , 40 , 55 , 60 , 38 , 25 , 7 , 78.

Step 1: 

The first three elements  20 , 30 , 35 are added to a node.

s1

Step 2:

The element 85 is added to the node. Now if we jump back to the previous section we can see that a B-tree with degree t=2 can have at most 3 key values. Thus the node is split from the median.

Note: How to calculate median for splitting the node-

  • Let x be a given key values in a node. 
  • n be the length of the node .
  • Meadian = n[x] / 2.

Hence here we can see the length n[x] = 4.

Thus, Median =  n[x] / 2  => 4 / 2 = 2.

This means that the node will be split from the second key of the node.

s2

Step 3:

As the node is split  30 becomes the new root node of the tree.

s3

Step 4:

The element 5 is inserted.

s4

Step 5:

The element 10 is inserted.

Step 6:

The element 40 is inserted

s6

Step 7:

The element 55 is added to the node.

Step 8:

  • To conserve the degree of the tree, we need to split the node where 55 was added. To do so we calculate the median which comes out to be 2.
  • The node is split from the 2nd key. 40 moves upwards to the root node.
  • The tree structure is shown as follows.
s8

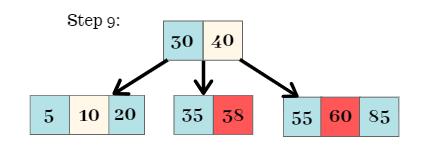
Step 9:

The elements 38 and 60 are added to the B-Tree.

s9

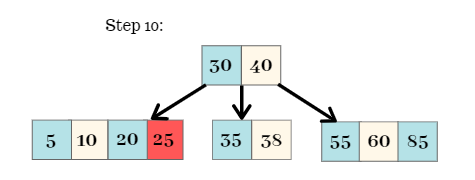
Step 10:

  • The element 25 is added to the node. The node has to split as each node in this tree can have at most 3 keys.
  • The node is split from the Median, i.e, 2.
s10

Step 11:

The node is split from the 2nd key. Thus, 10 moves upwards to the parent / root node.

s11

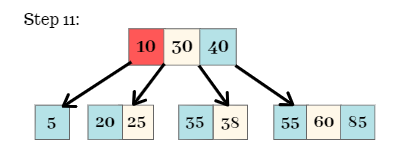
Step 12:

The elements 7 and 78 are added to the B-Tree

s12

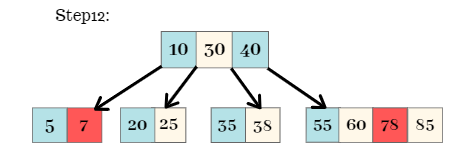
Step 13:

  • As the node is split the element 60 moves upward towards the parent / root node.
  • Now, again we can see that the root node is to be split because each node can hold at most 3 keys.
s13

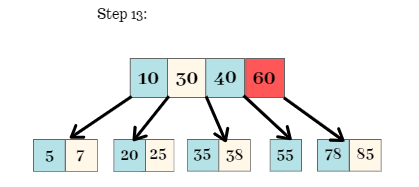
Step 14:

  • Again, we calculate the median of the node. The median can be calculated as follows,
    • Median = n[x]  /  2.
    • Median = 4 / 2.
    • Median = 2.
  • The node is split from the 2nd key which moves upwards and becomes the new root of the tree. The tree structure that follows is shown as follows,
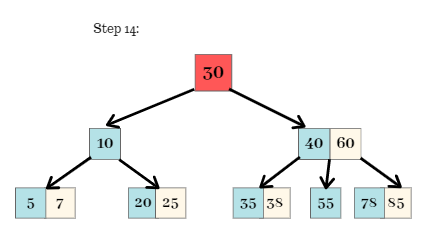
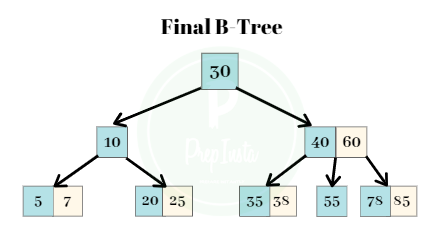
  • The final B-Tree after the concurrent insertion and splitting is shown as follows.
  • This B-Tree fulfills all the properties of a B-Tree.
  • Each node has either at least 1 key or at most 3 keys.
  • Any node with number of keys exceeding the given number is split and re-arranged accordingly.
final

One comment on “B- Trees”