C++ Program to Minimize the maximum difference between heights
Minimize the maximum difference between heights in C++
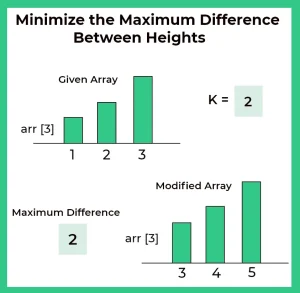
Here, in this page we will discuss the program to minimize the maximum difference between heights in C++ . We are Given with heights of n towers and a value k. We need to either increase or decrease the height of every tower by k (only once) where k > 0. Our task is to minimize the difference between the heights of the longest and the shortest tower after modifications and output this difference.

Algorithm :
- Take the size of the array from the user and store it in a variable say n and take the value of K and store it in another variable say k.
- Now declare an array of size n and take n elements of the array from the user.
- Now, create one function to perform the required operation.
- First, we try to sort the array and make each height of the tower maximum.
- We do this by decreasing the height of all the towers towards the right by k and increasing all the height of the towers towards the left (by k).
- It is also possible that the tower you are trying to increase the height doesn’t have the maximum height.
- Therefore we only need to check whether it has the maximum height or not by comparing it with the last element towards the right side which is a[n]-k.
- Since the array is sorted if the tower’s height is greater than the a[n]-k then it’s the tallest tower available.
- Similar reasoning can also be applied for finding the shortest tower.
Run
#include<bits/stdc++.h>
using namespace std;
int getMinDiff(int arr[], int n, int k){
if (n == 1)
return 0;
sort(arr, arr + n);
vector<pair<int, int>> t;
map<int, int> m;
int n_ = 1;
t.push_back(pair<int, int>(arr[0] + k, arr[0]));
t.push_back(pair<int, int>(arr[0] - k, arr[0]));
for (int i = 1; i < n; i++) {
if (arr[i] != arr[i - 1]) {
t.push_back(pair<int, int>(arr[i] + k, arr[i]));
t.push_back(pair<int, int>(arr[i] - k, arr[i]));
m[arr[i]] = 0;
n_++;
}
}
sort(t.begin(), t.end());
int l = 0, r = 0;
int ans = t[t.size() - 1].first - t[0].first;
int count = 0;
while (r < t.size()) {
while (r < t.size() and count < n_) {
if (m[t[r].second] == 0)
count++;
m[t[r].second]++;
r++;
}
if (r == t.size() and count < n_)
break;
ans = min(ans, t[r - 1].first - t[l].first);
while (l <= r and count >= n_) {
if (m[t[l].second] == 1)
count--;
m[t[l].second]--;
ans = min(ans, t[r - 1].first - t[l].first);
l++;
}
}
return ans;
}
int main()
{
int arr[] = {1, 10, 14, 14, 14, 15};
int n = sizeof(arr)/sizeof(arr[0]);
int k = 6;
cout << getMinDiff(arr, n, k);
}Output :
5
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription






Login/Signup to comment