Program to find Median of two sorted arrays of equal size in C++

October 13, 2022

Median of two sorted arrays of equal size in C++

Here, in this page we will discuss the program to find median of two sorted arrays of equal size in C++ programming language. We are given with two arrays say arr1[] and arr2[] of the same size say n . We need to find the median after merging these arrays.

Median of two sorted arrays of equal size in C++

Method 1:

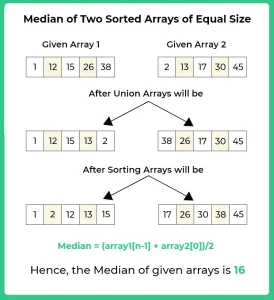
  • Find the union of the given two arrays.
  • Sort both array 1 and array2 (Using inbuilt sort() function).
  • Then the median element will be
    Median = (arr1[n-1]+arr2[0])/2

Time and Space Complexities :

  • Time-Complexity :O(nlogn)
  • Space-Complexity : O(1)
Median of two sorted arrays in C++

Code for Median of two Sorted arrays of equal size in C++

Run 
#include<bits/stdc++.h>
using namespace std;

int getMedian(int ar1[], int ar2[], int n)
{
    int j = 0;
    int i = n - 1;
    while (ar1[i] > ar2[j] && j < n && i > -1)
        swap(ar1[i--], ar2[j++]);

    sort(ar1, ar1 + n);
    sort(ar2, ar2 + n);

    return (ar1[n - 1] + ar2[0]) / 2;
}





int main()
{
   int n;
   cin>>n;

   int arr1[n], arr2[n];
   for(int i=0; i<n; i++)
      cin>>arr1[i];

   for(int i=0; i<n; i++)
      cin>>arr2[i];

   cout<<getMedian(arr1, arr2, n);

   return 0;
}
Input :
5
1 12 15 26 38
2 13 17 30 45

Output :
16

Given an array which consists of only 0, 1 and 2

Move all the negative elements to one side of the array

Minimum no. of Jumps to reach the end of an array 

Find Largest sum contiguous Subarray

Minimize the maximum difference between heights 

Method 2 :

  • Take the size of the array from the user and store them in the variables say n.
  • Create two arrays of size n and then take elements of the respective arrays from the user.
  • Now, create variable count. Keep track of count while comparing elements of two arrays.
  • Run a loop that will terminate when count > n.
  • If count becomes n(For 2n elements), we have reached the median.
  • Take the average of the elements at indexes n-1 and n in the merged array.

Time and Space Complexities :

  • Time-Complexity :O(n)
  • Space-Complexity : O(1)

Code for Median of two Sorted arrays of equal size in C++

Run 
#include <bits/stdc++.h>
using namespace std;

int getMedian(int ar1[], int ar2[], int n)
{
    int i = 0;
    int j = 0;
    int count;
    int m1 = -1, m2 = -1;

    for (count = 0; count <= n; count++){
        if (i == n){
           m1 = m2;
           m2 = ar2[0];
           break;
    }
    else if (j == n){
          m1 = m2;
          m2 = ar1[0];
          break;
    }
    if (ar1[i] <= ar2[j]){
       /* Store the prev median */
       m1 = m2;
       m2 = ar1[i];
       i++;
    }
    else{
        /* Store the prev median */
        m1 = m2;
        m2 = ar2[j];
        j++;
     }
  }
   return (m1 + m2)/2;
}

// Driver Code
int main()
{
   int n;
   cin>>n;

   int arr1[n], arr2[n];

   for(int i=0; i<n; i++)
      cin>>arr1[i];

   for(int i=0; i<n; i++)
      cin>>arr2[i];

   getMedian(arr1, arr2, n);

   return 0;
}



Input :
5
1 12 15 26 38
2 13 17 30 45

Output :
16

Method 3 (By comparing the median of the two arrays-Divide and Conquer) :

  • Find the medians of the given two arrays and store them in variable say m1 and m2.
  • Now, if m1=m2, then that will be the required output.
  • If m1>m2, then we check in the subarrays, arr1[0 – middle element] and in arr2[middle element – last].
  • If m2>m1, then we check in the subarrays, arr1[middle element – last] and in arr2[0-middle element ].
  • This will be the recursive process and repeat this till size of both the arrays become 2.
  • As, when the size will be 2 , we can use the formula :

    Median = (max(ar1[0], ar2[0]) + min(ar1[1], ar2[1]))/2

Time and Space Complexities :

  • Time-Complexity :O(logn)
  • Space-Complexity : O(1)

Code for Median of two Sorted arrays of equal size in C++

Run 
#include<bits/stdc++.h>
using namespace std;
/* Function to get median of a sorted array */
int median(int arr[], int n)
{
   if (n%2 == 0)
    return (arr[n/2] + arr[n/2-1])/2;
   else
    return arr[n/2];
}

int getMedian(int ar1[], int ar2[], int n)
{

    if (n == 1)
      return (ar1[0] + ar2[0])/2;
    if (n == 2)
      return (max(ar1[0], ar2[0]) + min(ar1[1], ar2[1])) / 2;

    int m1 = median(ar1, n); 
    int m2 = median(ar2, n); 

    if (m1 == m2)
     return m1;

    if (m1 < m2)
    {
       if (n % 2 == 0)
         return getMedian(ar1 + n/2 - 1, ar2, n - n/2 +1);
       return getMedian(ar1 + n/2, ar2, n - n/2);
    }

    if (n % 2 == 0)
      return getMedian(ar2 + n/2 - 1, ar1, n - n/2 + 1);
    return getMedian(ar2 + n/2, ar1, n - n/2);
}

int main()
{
   int n;
   cin>>n;

   int arr1[n], arr2[n];
   for(int i=0; i<n; i++)
    cin>>arr1[i];

   for(int i=0; i<n; i++)
     cin>>arr2[i];

   cout<<getMedian(arr1, arr2, n);

   return 0;
}
Input :
5
1 12 15 26 38
2 13 17 30 45

Output :
16

Prime Course Trailer

Related Banners

Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription

Get Prime
While loop in C