Heap Sort in C++

June 4, 2022

What is heap sort in C++?

A heap is a complete binary tree which is represented using array or sequential representation. It is one of the efficient algorithm for sorting given data in logical order.

In this sorting algorithm a tree structure called heap is used where a heap is a type of binary tree. An ordered balanced binary tree is called a Min-heap, where the value at the root of any subtree is less than or equal to the value of either of its children. An ordered balanced binary tree is called a max heap where the value at the root of any subtree is more than or equal to the value of either of its children. In this article, we will learn more about heap sort in C++

 

Heap Sort algorithm in C++

Working of heap sort in C++

To sort any list into a logical order following steps are followed :-

  • Convert the list into heap.
  • Now convert this heap into max heap.
  • As the heap is converted to max heap largest element in the list is stored in the root of the heap, replace it with the last item of the heap.
  • Now delete this node and reduce the size of heap by 1.
  • Follow these steps until the list is sorted.

How to convert given list into heap ?

Let say, the index of any element in the list is i, the element in the index 2i+1 will become the left child and element in 2i+2 index will become the right child. And we want to find out the parent of any element then we can find it by finding the lower bound which is given by (i-1)/2 .

 

Heap sort in C++

 

Algorithm for heap sort in C++

MAX-HEAPIFY(A,i)
    1- i<-left[i]
    2- r<-right[i]
    3- if l<heap-size[A]and A[l]>A[i]
    4- then largest<-1
    5- else largest<-i
    6- if r<heap-size[A] and A[r]>A[largest]
    7- then largest<-r
    8- if largest!=i
    9- then exchange A[i]<->A[largest]
    10- MAX-HEAPIFY[A,largest]

HEAP-SORT(A)
    1- BUILD-MAX-HEAP(A)
    2- for i<-length[A] down to 2
    3- do exchange A[1]<-> heap-size[A]-1
    4- heap-size[A]<-heap-size[A]-1
    5- MAX-HEAPIFY(A,1)

BUILD-MAX-HEAP(A)
    1- heap-size[A]<-length[A]
    2- for i<-(length[A]/2) down to 1 do
    3- MAX-HEAPIFY(A,i)

Program for heap sort in C++

Run
#include<iostream>

using namespace std;

void heapify(int arr[], int n, int i)
{
    int largest = i;
    int l = 2*i + 1;
    int r = 2*i + 2;
 
    //If left child is larger than root
    if (l < n && arr[l] > arr[largest])
        largest = l;
 
    //If right child largest 
    if (r < n && arr[r] > arr[largest])
        largest = r;
 
    //If root is nor largest
    if (largest != i)
    {
        swap(arr[i], arr[largest]);
 
        //Recursively heapifying the sub-tree
        heapify(arr, n, largest);
    }
}

void heapSort(int arr[], int n)
{
    
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
 
    //One by one extract an element from heap
    for (int i=n-1; i>=0; i--)
    {
        //Moving current root to end
        swap(arr[0], arr[i]);
 
        //Calling max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}
 
//Function to print array
void display(int arr[], int n)
{
    for (int i = 0; i < n; i++)
    {
        cout << arr[i] << "\t";
    }
    cout << "\n";
}
 

int main()
{
    int arr[] = {1, 14, 3, 7, 0};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout << "Unsorted array  \n";
    display(arr, n);
    
    heapSort(arr, n);
 
    cout << "Sorted array  \n";
    display(arr, n);
}
Output:
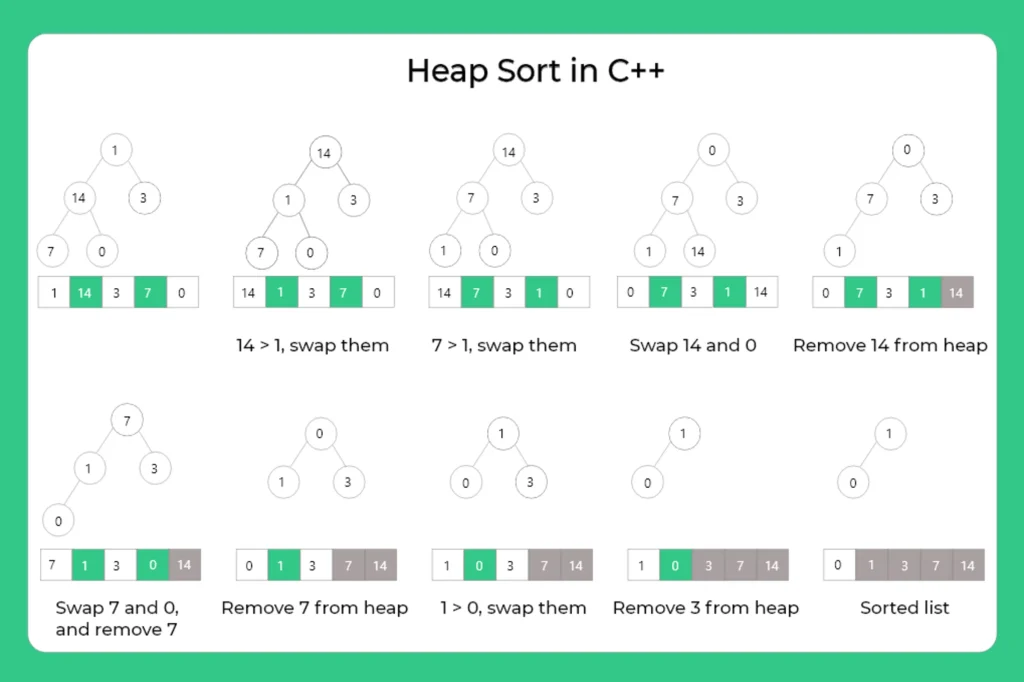
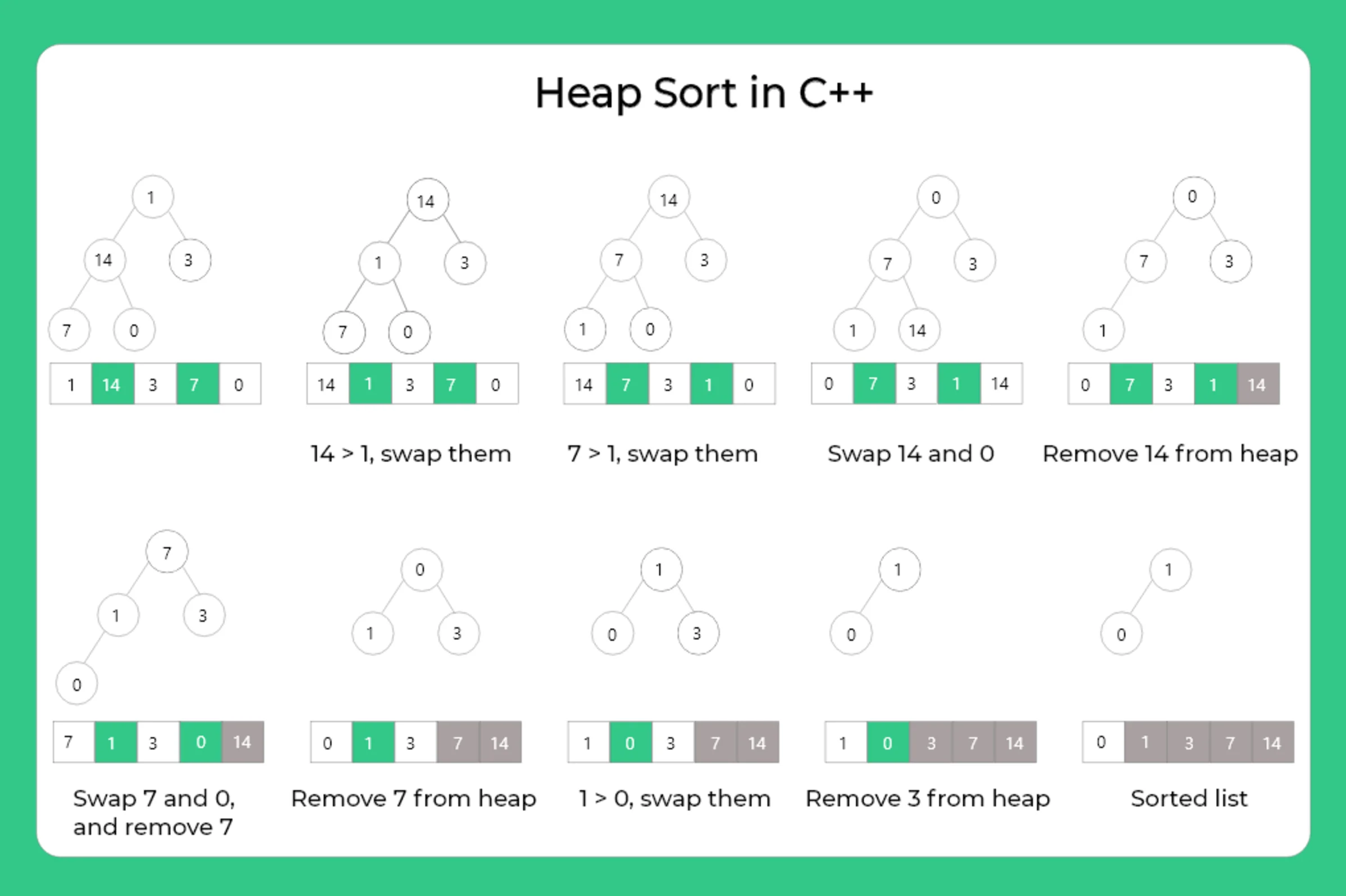
Unsorted array  
1	14	3	7	0	
Sorted array  
0	1	3	7	14

Time Complexity
For Heap sort in C++

Best

O(nlog n)

Average

O(nlog n)

Worst

O(nlog n)

Quiz time

Quiz Time

Question 1.Which of the following sorting algorithms in its typical implementation gives best performance when applied on a sorted array?

  1. Quick Sort
  2. Heap Sort
  3. Insertion Sort
  4. Merge
Insertion sort takes linear time when input array is sorted or almost sorted. All other sorting algorithms mentioned above will take more than linear time in their typical implementation.
 
Ans. Insertion Sort (C)
 

Question 2. What is the time complexity of Build Heap operation. Which is used to create a max(or min) binary heap from a given array.?

  1. O(n)
  2. O(log n)
  3. O(nlog n)
  4. None of the above
BUILD-HEAP(A) 
    heapsize := size(A); 
    for i := floor(heapsize/2) downto 1 
        do HEAPIFY(A, i); 
    end for 
END

Although the worst case complexity looks like O(nLogn), upper bound of time complexity is O(n).

Ans: A