Boyer–Moore Majority Vote Algorithm

March 25, 2025

Boyer-Moore majority vote algorithm

On this page we will discuss about Boyer–Moore majority vote algorithm in C++ . The Boyer-Moore Majority Vote Algorithm is an efficient algorithm for finding the majority element in an array, which refers to an element that occurs more than half of the time in the array. So lets see this in detail with code in C++ .

Boyer-Moore Majority Vote Algorithm in C_

Boyer-Moore Majority Vote Algorithm in C++

The Boyer-Moore Majority Vote Algorithm is an efficient algorithm for finding the majority element in an array, which is an element that appears more than n/2 times, where n is the length of the array. The algorithm was proposed by Robert S. Boyer and J Strother Moore in 1980 and is widely used in various applications, such as data analysis, voting systems, and image processing.

The Boyer-Moore Majority Vote Algorithm operates in linear time complexity, which makes it efficient for large arrays, and uses constant space. The basic idea of the algorithm is to maintain a counter that starts from zero and iterates through the array, incrementing the counter for each occurrence of a candidate element, and decrementing it for each occurrence of a different element. The algorithm identifies the majority element as the candidate element with the highest count after scanning through the array.

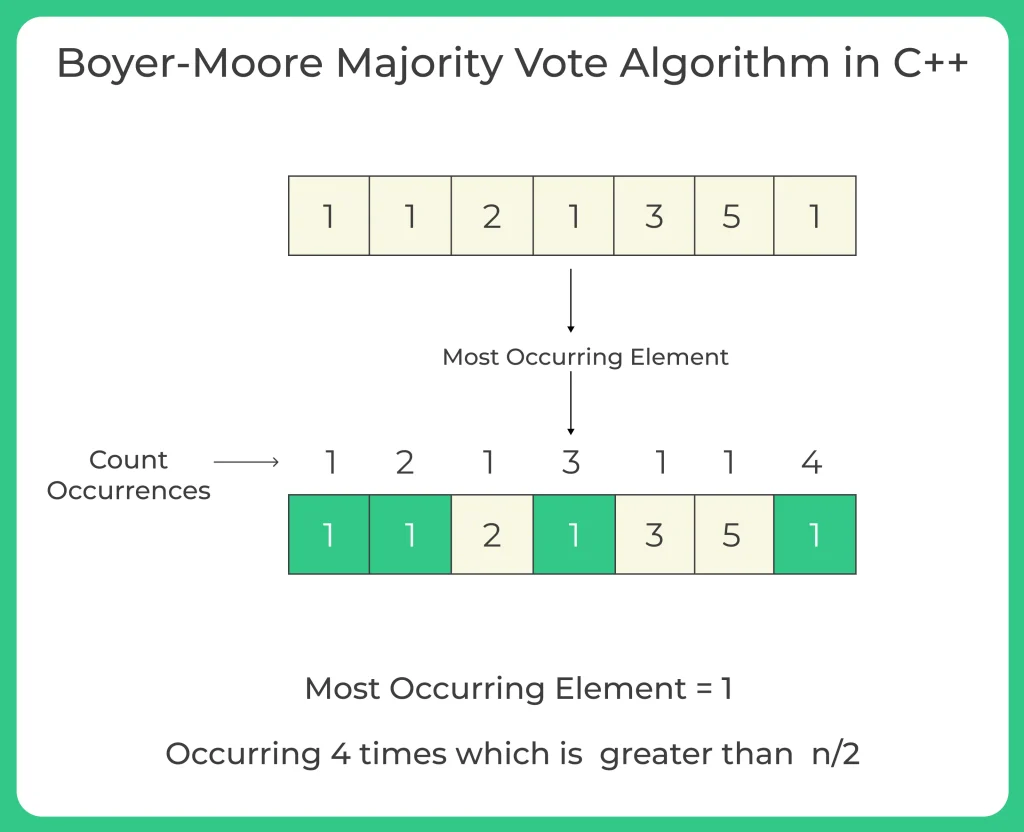
Boyer-Moore Majority Vote Algorithm in C++

Example:

Input: k = 6,  arr = [ 1, 2, 5, 2, 2, 2 ]

Output: Majority Element is 2

Sort the array in Waveform

Sorting of Array

Majority Element in Array

Largest Sum Contigous SubArray

K-pairs with smallest sum in 2 arrays

Algorithm :

  1. Iterate through the array from the beginning to the end.
  2. For each element in the array:
    • If the count is 0, set the current element as the candidate.
    • If the current element is the same as the candidate, increment the count.
    • If the current element is different from the candidate, decrement the count.
  3. After the first pass, the candidate is the potential majority element.
  4. Reset the count to 0.
  5. Iterate through the array again.
  6. Count the occurrences of the candidate element.
  7. If the candidate occurs more than half of the time, it is the majority element.
  8. If the candidate occurs more than half of the time, return it as the majority element.
  9. If the candidate occurs less than or equal to half of the time, there is no majority element.

C++ Code

Run 
#include <iostream>
#include <vector>

using namespace std;

int majorityElement (vector < int >&nums)
{
  int candidate = 0;		// Initialize candidate as the first element
  int count = 0;		// Initialize count as 0

  // First pass: Find the potential majority element
for (int num:nums)
    {
      if (count == 0)
	{
	  candidate = num;	// Set candidate as the current element
	}
      count += (num == candidate) ? 1 : -1;	// Increment or decrement count
    }

  // Second pass: Verify if the candidate is the majority element
  count = 0;			// Reset count
for (int num:nums)
    {
      if (num == candidate)
	{
	  count++;		// Count occurrences of the candidate
	}
    }

  // If the candidate occurs more than half of the time, return it
  if (count > nums.size () / 2)
    {
      return candidate;
    }
  else
    {
      return -1;		// Return -1 if there is no majority element
    }
}

int main ()
{
  // Example usage of the Boyer-Moore Majority Vote Algorithm
  vector < int >nums = { 1, 2, 2, 2, 3, 2, 4, 2, 5 };	// Example input array
  int majority = majorityElement (nums);	// Call the algorithm
  if (majority != -1)
    {
      cout << "The majority element is: " << majority << endl;
    }
  else
    {
      cout << "There is no majority element." << endl;
    }

  return 0;
}

Output

The majority element is: 2