Array Rotation in C++
Rotation of array in C++
On this page we will discuss about rotation of array in C++ . Array rotation is a process of rearranging the elements of an array by shifting its elements by a specified number of positions.This can be done in two ways: left rotation and right rotation.
Array Rotation In C++ Programming
Array rotation is a common operation in computer programming that involves shifting the elements of an array by a certain number of positions. This can be done in two ways: left rotation and right rotation.
- In left rotation, the elements of the array are shifted to the left by a certain number of positions, and the elements that “fall off” the left end of the array are added to the right end of the array. For example, if we have an array [1, 2, 3, 4, 5] and we left rotate it by 2 positions, we would get the array [3, 4, 5, 1, 2].
- In right rotation, the elements of the array are shifted to the right by a certain number of positions, and the elements that “fall off” the right end of the array are added to the left end of the array. For example, if we have an array [1, 2, 3, 4, 5] and we right rotate it by 2 positions, we would get the array [4, 5, 1, 2, 3].
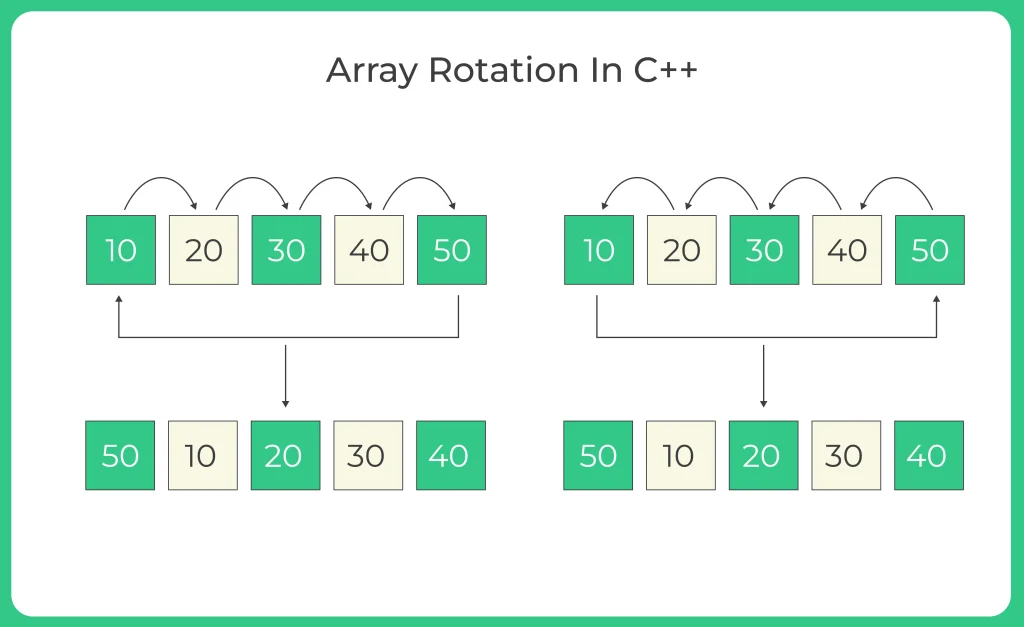
Algorithm for ( Using a Temporary Array )
- Create a temporary array of size d.
- Copy the first d elements of the original array to the temporary array.
- Shift the remaining elements of the original array to the left by d positions.
- Add the elements from the temporary array to the right end of the original array.
- The array is now left rotated by d positions.
C++ code for temporary array method
Run
#include <iostream>
using namespace std;
void leftRotate (int arr[], int n, int d)
{
int temp[d];
for (int i = 0; i < d; i++)
{
temp[i] = arr[i];
}
for (int i = d; i < n; i++)
{
arr[i - d] = arr[i];
}
for (int i = n - d, j = 0; i < n; i++, j++)
{
arr[i] = temp[j];
}
}
void rightRotate (int arr[], int n, int d)
{
int temp[d];
for (int i = n - d, j = 0; i < n; i++, j++)
{
temp[j] = arr[i];
}
for (int i = n - d - 1; i >= 0; i--)
{
arr[i + d] = arr[i];
}
for (int i = 0; i < d; i++)
{
arr[i] = temp[i];
}
}
int main ()
{
int arr[] = { 1, 2, 3, 4, 5 };
int n = sizeof (arr) / sizeof (arr[0]);
int d = 2;
cout << "Original Array: ";
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
cout << endl;
leftRotate (arr, n, d);
cout << "Left Rotated Array: ";
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
cout << endl;
rightRotate (arr, n, d);
cout << "Right Rotated Array: ";
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
Output
Original Array: 1 2 3 4 5 Left Rotated Array: 3 4 5 1 2 Right Rotated Array: 1 2 3 4 5
Algorithm for ( Rotating One by One )
- For each rotation, store the first element of the array in a temporary variable.
- Shift all the remaining elements of the array one position to the left.
- Move the temporary variable to the end of the array.
- Repeat the above steps d times to left rotate the array by d positions.
C++ code for rotating one by one
Run
#include <iostream>
using namespace std;
void leftRotate (int arr[], int n, int d)
{
for (int i = 0; i < d; i++)
{
int temp = arr[0];
for (int j = 0; j < n - 1; j++)
{
arr[j] = arr[j + 1];
}
arr[n - 1] = temp;
}
}
void rightRotate (int arr[], int n, int d)
{
for (int i = 0; i < d; i++)
{
int temp = arr[n - 1];
for (int j = n - 1; j >= 1; j--)
{
arr[j] = arr[j - 1];
}
arr[0] = temp;
}
}
int main ()
{
int arr[] = { 1, 2, 3, 4, 5 };
int n = sizeof (arr) / sizeof (arr[0]);
int d = 2;
cout << "Original Array: ";
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
cout << endl;
leftRotate (arr, n, d);
cout << "Left Rotated Array: ";
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
cout << endl;
rightRotate (arr, n, d);
cout << "Right Rotated Array: ";
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}
Output
Original Array: 1 2 3 4 5 Left Rotated Array: 3 4 5 1 2 Right Rotated Array: 1 2 3 4 5
Prime Course Trailer
Related Banners
Get PrepInsta Prime & get Access to all 200+ courses offered by PrepInsta in One Subscription
Get over 200+ course One Subscription
Courses like AI/ML, Cloud Computing, Ethical Hacking, C, C++, Java, Python, DSA (All Languages), Competitive Coding (All Languages), TCS, Infosys, Wipro, Amazon, DBMS, SQL and others
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal Line by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric – C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree- C | C++ | Java
Introduction to Trees
Binary Trees
- Binary Tree in Data Structures (Introduction)
- Tree Traversals: Inorder Postorder Preorder : C | C++ | Java
- Inorder Postorder PreOrder Traversals Examples
- Tree Traversal without Recursion
Binary Search Trees
Traversals
- Traversal in Trees
- Tree Traversals: Breadth-First Search (BFS) : C | C++ | Java
- Tree Traversals: Depth First Search (DFS) : C | C++ | Java
- Construct a Binary Tree from Postorder and Inorder
B – Trees
AVL Trees
- AVL Trees
Complete Programs for Trees
- Depth First Traversals – C | C++ | Java
- Level Order Traversal – C | C++ | Java
- Construct Tree from given Inorder and Preorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Inorder traversals – C | C++ | Java
- Construct Tree from given Postorder and Preorder traversal – C | C++ | Java
- Find size of the Binary tree – C | C++ | Java
- Find the height of binary tree – C | C++ | Java
- Find maximum in binary tree – C | C++ | Java
- Check whether two tree are identical- C| C++| Java
- Spiral Order traversal of Tree- C | C++| Java
- Level Order Traversal LIne by Line – C | C++| Java
- Hand shaking lemma and some Impotant Tree Properties.
- Check If binary tree if Foldable or not.- C| C++| Java
- check whether tree is Symmetric C| C++| Java.
- Check for Children-Sum in Binary Tree- C|C++| Java
- Sum of all nodes in Binary Tree- C | C++ | Java
- Lowest Common Ancestor in Binary Tree. C | C++ | Java
Login/Signup to comment