Maximum size square sub-matrix with all 1s

December 7, 2021

Maximum size square sub-matrix with all 1s

In maximum size square sub-matrix with all 1s problem, we have to find the largest square matrix with all ones in the given matrix. This article provides a C++ solution with an explanation.

Maximum size square sub-matrix with all 1s Problem Description

Maximum size square sub-matrix with all 1s Problem Description

Given a r*c matrix with each value as either 0 or 1. Return the side of the largest square sub matrix with all ones.

Input:

  • First line contains two integers – the dimension of input matrix (row,col).
  • Next r lines contains c integers each – values of each cell of the matrix.

Output:

  • Single integer the side of largest square with all 1s.

Example

Input

  • 5 5
  • 0 1 1 0 1
  • 1 1 0 1 0
  • 0 1 1 1 0
  • 1 1 1 1 0
  • 1 1 1 1 1
Output
  • 3
Explanation
  • The square from (2,1) to (4,3) is the largest with all 1s.

Maximum size square sub-matrix with all 1s Solution

Brute Force Solution

We will iterate over every possible square sub matrix and check whether that matrix has all 1s or not. The time complexity of just iterating over all squares is O(row*col*max(row,col)) & time complexity of check a square is O(row*col). It is obvious that this solution would timeout.

Dynamic Programming Solution

In this solution we try to think if while checking a particular square if we can reuse previously checked squares.

Algorithm

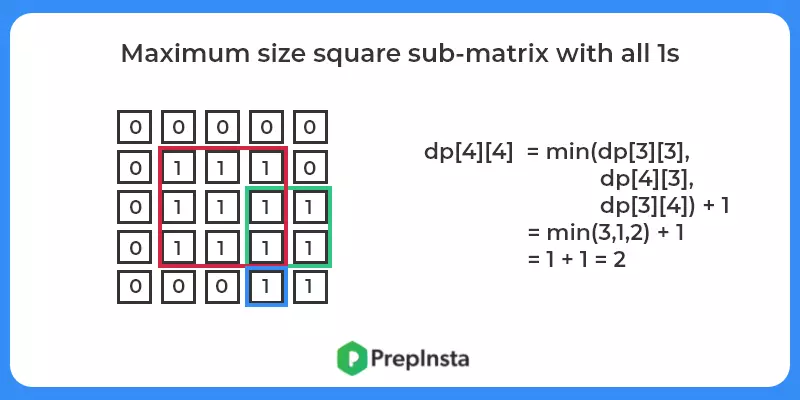
  • Create a dp table of dimension (row,col) where dp[i][j] = side of maximum square possible with bottom right corner at (i,j).
  • Now while calculating dp[i][j], our transitions can be –

If(mat[i][j]==0)

dp[i][j] = 0 {as no square is possibl}

else

dp[i][j] = 1 + min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])  {Taking diagonally upward, left & upward squares.}

  • The first row and column of the dp table will act as base case.
  • Now just iterate over the table and find the maximum value.

Time Complexity – O(row*col)

Space Complexity – O(row*col)

Maximum size square sub-matrix with all 1s Tansitions Example

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int mat[N][N];
int dp[N][N];
int r, c;
int area()
{
    int ans = 0; // stores the maximum answer

    // Copy first column
    for (int i = 0; i < r; i++)
    {
        dp[i][0] = mat[i][0];
        ans = max(ans, dp[i][0]);
    }

    // Copy first row
    for (int i = 0; i < c; i++)
    {
        dp[0][i] = mat[0][i];
        ans = max(ans, dp[0][i]);
    }

    for (int i = 1; i < r; i++)
    {
        for (int j = 1; j < c; j++)
        {
            if (mat[i][j] == 1)
            {                   // Diagonally Upward square
                dp[i][j] = 1 + min(dp[i – 1][j – 1], // Left & upward square
                                   min(dp[i][j – 1], dp[i – 1][j]));
            }
            else
            {
                dp[i][j] = 0;
            }

            ans = max(ans, dp[i][j]);
        }
    }

    return ans;
}
int main()
{
    cin >> r >> c;
    for (int i = 0; i < r; i++)
    {
        for (int j = 0; j < c; j++)
        {
            cin >> mat[i][j];
        }
    }

    cout << area() << endl;

    return 0;
}

Output

5 5
0 1 1 0 1
1 1 0 1 0
0 1 1 1 0
1 1 1 1 0
1 1 1 1 1
3