Matrix Chain Multiplication C++ Implementation

November 6, 2021

Matrix Chain Multiplication C++ Implementation

In matrix chain multiplication we are given a list containing the dimensions ie the row and column of some matrices. The idea is to calculate the minimum number of operations we can perform to multiply those matrices. Here we provide c++ implementation with top down and bottom up solution to the problem.

Matrix Chain Multiplication Problem Description

We are given a list of matrices and we have to find the most optimal way to multi the matrices together.

Input Format:

First line contains an integer n denoting the size of an array.

Next line contains n integers. Dimension of a matrix are represented by adjacent values of the array ie F[i-1] , F[i] represent Row , Column of a matrix. This means we have n-1 matrices in total.

Prerequisites:

The following are the prerequisites –

To understand the solution we have to first understand how matrix multiplication works. Let us say we are given two matrices M1 with dimensions r1 & c1 and M2 with dimensions r2 & c2. The condition that M1*M2 exists is c1 should be equal to r2. The resultant matrix of M1*M2 will have dimensions of r1 & c2.
To calculate single element of M1*M2 we have to multiply c1 elements of M1 with r2 elements of M2. This means we performed c1 (as r2 as c1 is equal to r2) operations of multiplication. This means to find r1*c2 ( number of elements in M1*M2) we need r1*c1*c2 operations.

Matrix Chain Multiplication Solution (Memorization):

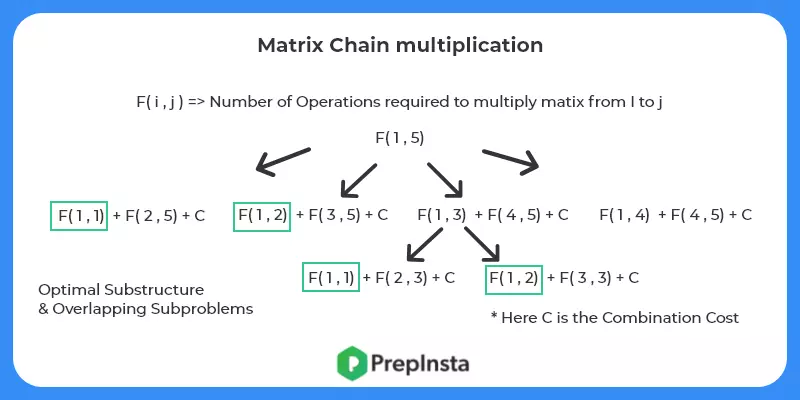
To form a top down (or memorized solution) we try to break down the problem recursively.

We define F(i,j) as number of operations required to solve matrices from i to j . Recursively F(i,j) = min(F(i,k)+F(k+1,j) + C ) where K belongs to [i,j-1] and C is the combination cost. From above we can easily find C.

It is easy to see that there optimal substructure and over lapping sub problems in the above solution.

Refer to code below for more details.

C++ Code:

#include <bits/stdc++.h>
using namespace std;
int dp[105][105];
int f(int arr[], int i, int j)
{
    /*
        Base Case if j<=i
    */
    if (j <= i)
        return 0;
    if (dp[i][j] != –1)
        return dp[i][j];
    int ans = INT_MAX;

    for (int k = i; k < j; k++)
    {
        /* 
            Diving into subproblems and taking minimum 
        */
        int cur = f(arr, i, k) + f(arr, k + 1, j) + arr[i – 1] * arr[k] * arr[j];
        ans = min(ans, cur);
    }

    return dp[i][j] = ans;
}
int main()
{
    memset(dp, –1, sizeof dp);
    int arr[] = {1, 2, 3};
    int n = sizeof(arr) / sizeof(arr[0]);

    cout << “Result :” << f(arr, 1, n – 1) << endl;
    return 0;
}

Output:

Result :6

Matrix Chain Multiplication Solution (Bottom Up)

The bottom up solution is similar to above. Here we instead of solving larger problem we solve smaller problem first ie we first solve for smaller length.

C++ Code

#include <bits/stdc++.h>
using namespace std;
int f(int p[], int n)
{
    int dp[n][n];
    /* 
        dp[i][j] means cost of multilying from i to j
    */
    // Multilying COst of single matix is 0
    for (int i = 0; i < n; i++)
        dp[i][i] = 0;
 
    for (int length = 2; length < n; length++)
    {
        // Solving for smaller length to bigger length
        for (int i = 1; i < n – length + 1; i++)
        {
            int j = i + length – 1;
            dp[i][j] = INT_MAX;
            for (int k = i; k < j; k++)
            {
                // Using already solved smaller sub problems
                int cur = dp[i][k] + dp[k + 1][j] + p[i – 1] * p[k] * p[j];
                dp[i][j] = min(dp[i][j], cur);
            }
        }
    }
 
    return dp[1][n – 1];
}
int main()
{
    int arr[] = {1, 2, 3};
    int n = sizeof(arr) / sizeof(arr[0]);
 
    cout << “Result :” << f(arr, n) << endl;
    return 0;
}

Output:

Result :6