Longest Palindromic Subsequence

November 6, 2021

Longest Palindromic Subsequence

In Longest Palindromic Subsequence problem we are given a string and are asked to find length of the longest palindromic subsequence. In this article we provide a C++ implementation with explanation of the solution.

Longest Palindromic Subsequence Problem Desciption

Longest Palindromic Subsequence Problem Description

In this problem we are given a input string consisting of english alphabets. We have to return the length a longest palindromic subsequence possible. A subsequence is a string that is formed by removing any number of characters (including 0) from the input string.

Input:

  • Single line input containing an input string.

Output:

  • Longest length required.

Longest Palindromic Subsequence Solution

Solution 1 (Memoization):

  • Break Down the Problem – In this step we try to break down the problem into smaller problems and assume recursion will solve the smaller problems.

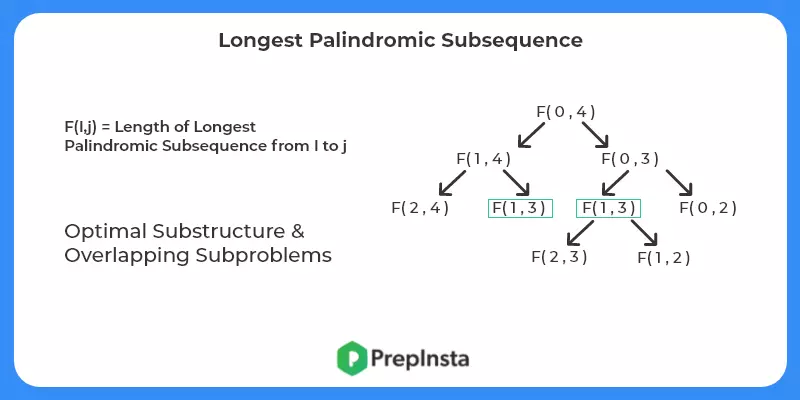
F(i,j) = Length of longest Palidromic Subsequence starting from i till j index.

           Now there are two cases possible:

F(i,j) = 2+ F(i+1,j-1)   { if s[i]==s[j]}

Or

F(i,j) = max(F(i+1,j),F(i,j-1)) { if s[i]!=s[j]}

Longest Palindromic Subsequence Recusive Calls
  • Find the base case –  What can be base case? It’s easy find the solution to smallest known problem. Here we know solution for length 1 ie (i==j) and length 2 ie (i+1==j).
  • Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
Longest Palindromic Subsequence Memoization

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int memo[N][N];
string s;
int solve(int i, int j)
{
    if (i == j)
        return 1;
    if (i + 1 == j && s[i] == s[j])
        return 2;
    if (memo[i][j] != –1)
        return memo[i][j];
    if (s[i] == s[j])
        return memo[i][j] = 2 + solve(i + 1, j – 1);

 

    int op1 = solve(i + 1, j);
    int op2 = solve(i, j – 1);

 

    return memo[i][j] = max(op1, op2);
}
int main()
{
    cout << “Enter input string :”;
    cin >> s;
    memset(memo, –1, sizeof memo);
    cout << “Longest length is “ << solve(0, s.length() – 1) << endl;
    return 0;
}

Output

Enter input string :azbyncdcwbmaqx
Longest length is 7

Solution (Bottom Up Dynamic Programming)

In above solution we created a function that recursively solves smaller problems. Here we create a lps table and solve problems of smaller length first. In other words we find longest palindromic subsequence for sub strings of length = 1, then for length = 2 and so on.

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int memo[N][N];
string s;
int solve()
{
    int n = s.length();
    int lps[n][n];

 

    for (int i = 0; i < n; i++)
        lps[i][i] = 1;

 

    for (int length = 2; length <= n; length++)
    {
        for (int i = 0; i <= n – length; i++)
        {
            int j = i + length – 1;
            if (length == 2 && s[i] == s[j])
                lps[i][j] = 2;
            else if (s[i] == s[j])
                lps[i][j] = 2 + lps[i + 1][j – 1];
            else
                lps[i][j] = max(lps[i][j – 1], lps[i + 1][j]);
        }
    }

 

    return lps[0][n – 1];
}
int main()
{
    cout << “Enter input string :”;
    cin >> s;
    memset(memo, –1, sizeof memo);
    cout << “Longest length is “ << solve() << endl;
    return 0;
}

Output

Enter input string :azbyncdcwbmaqx
Longest length is 7