Fibonacci numbers

November 25, 2021

Fibonacci numbers

Fibonacci numbers is a basic question that introduces the concept of dynamic programming. In this article, we have provided C++ solution with explanation.

Fibonacci numbers problem description

Fibonacci Numbers Problem Description

Given a single integer n, output the nth Fibonacci number. Take 0 as 0th Fibonacci number.

Input:

  • A single line containing integer n.

Output:

  • Single integer the required number.

Solution

Top-Down Solution

  • Break Down the Problem – In this step, we try to break down the problem into smaller problems and assume recursion will solve the smaller problems. The recursive calls in Fibonacci numbers can be formed using their definition itself.

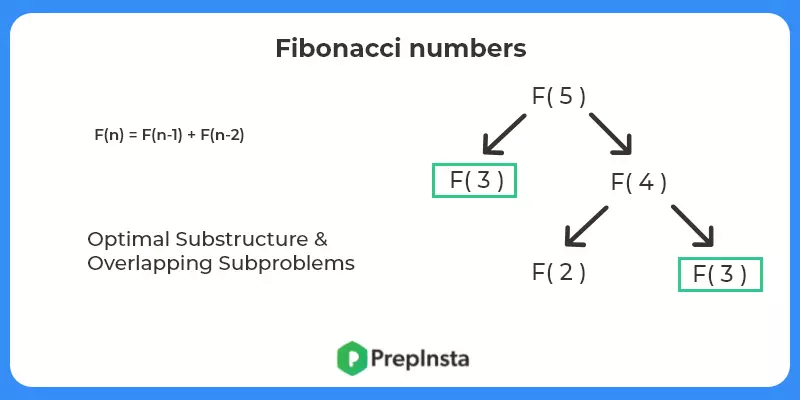
F(N) = F(N-1) +F(N-2)

  • Find the base case- The base case is the solution to the smallest known problem. Here we know F(0) = 0 & F(1) = 1.
  • Check for optimal substructure and overlapping subproblems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping subproblems properties can be visualized below.

Time complexity (memoized solution) – O(n)

Space Complexity (memoized solution) – O(n)

Bottom Up Solution

We can use bottom up dynamic programming by creating a dp table and using same transitions as above.

Time complexity – O(n)

Space Complexity – O(n)

Space Optimized Solution

The above solution has a space complexity of O(n). It can be done in O(1). Refer to the code for more details.

Time complexity – O(n)

Space Complexity – O(1)

Fibonacci Numbers Subproblems

Code

#include <bits/stdc++.h>
using namespace std;
// top down solution
int memo[1005];
int f(int n)
{
    if (n <= 1)
        return n;
    if (memo[n] != –1)
        return memo[n];
    return memo[n] = f(n – 1) + f(n – 2);
}
// Bottom Up
int bottomUp(int n)
{
    int dp[n + 1];
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++)
        dp[i] = dp[i – 1] + dp[i – 2];
    return dp[n];
}
// Space optimized
int spaceOptimized(int n)
{
    if (n <= 1)
        return n;
    int cur = 1, prev = 0;
    for (int i = 2; i <= n; i++)
    {
        int next = cur + prev;
        prev = cur;
        cur = next;
    }
    return cur;
}
int main()
{
    memset(memo, –1, sizeof memo);
    cout<<f(5)<<endl;
    cout<<bottomUp(5)<<endl;
    cout<<spaceOptimized(5)<<endl;
    return 0;
}

Output

5
5
5