Binomial Coefficient Implementation in C++

November 6, 2021

Binomial Coefficient Implementation in C++

In Binomial Coefficient as the name suggests we are required to find out the binomial coefficient ie C(n,r). Here is a c++ implementation for both top down and bottom up approach.

 

Binomial Coefficient Problem Description

Binomial Coefficient Problem Description

We are given two integers n, r. We have to find the binomial coefficient C(n,r) which is the coefficient of x^r in the expansion of (1+x)^n.

Input:

  • First-line contains two integers n and r

Example: 

  • Given n = 5 and r = 3
  • Binomial Coefficient C(5,3) = 10

Explanation

  • C(5/3) = (5! )/(3! * 2!) = 120/(6*2) = 10

Binomial Coefficient Solution Explanation

To solve the problem first we must be aware of the following relation

C(n,r) = C(n-1,r-1) + C(n-1,r)

Solution (Top Down):

To build a top down solution we must follow the following steps –

  • Break Down the Problem – For getting the value of C(n,r) we need the value of C(n-1,r-1) and C(n-1,r). This becomes our recurrence relation – 

C(n,r) = C(n-1,r-1) + C(n-1,r)

  • Find the base case – We know that C(n,n) = 1 & C(n,0) = 1. Also We know that in C(n,r) n>=r. So these relations will form the base case.
  • Check for optimal substructure and overlapping sub problems – It is easy to see that the problem can be broken down into smaller problems. The optimal substructure and overlapping sub problems properties can be visualized below.
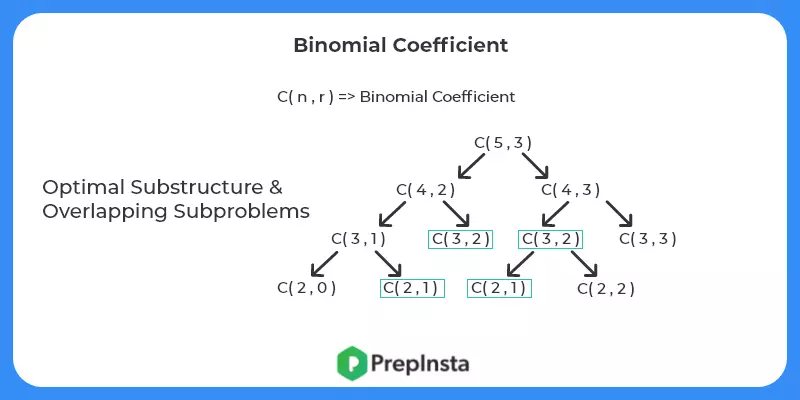
Binomial Coefficient Implementation in C++

Code C++:

#include <bits/stdc++.h>
using namespace std;
int C(int n, int r)
{
    if (r > n)
        return 0;

    if (r == 0 || r == n)
        return 1;

    int nCr = C(n – 1, r – 1) + C(n – 1, r);
    return nCr;
}
int main()
{
    int n, r;
    cout << “Enter n and r “;
    cin >> n >> r;
    cout << n << “C” << r << ” = “ << C(n, r) << endl;
    return 0;
}

Output:

Enter n and r 5 3
5C3 = 10

Solution (Bottom Up):

For bottom up solution we will use the smaller problems in the reverse direction. Refer to the code for more details.

C++ Code:

#include <bits/stdc++.h>
using namespace std;
int F(int n, int r)
{
    if (r > n)
        return 0;

    int C[n + 1][r + 1];

    for (int i = 0; i <= n; i++)
    {
        // j <= min(i,r) as in nCr n<=r
        for (int j = 0; j <= min(i, r); j++)
        {
            if (j == 0 || j == i)
                C[i][j] = 1;
            else
                C[i][j] = C[i – 1][j – 1] + C[i – 1][j];
        }
    }
    return C[n][r];
}
int main()
{
    int n, r;
    cout << “Enter n and r “;
    cin >> n >> r;
    cout << n << “C” << r << ” = “ << F(n, r) << endl;
    return 0;
}

Output:

Enter n and r 5 3
5C3 = 10

One comment on “Binomial Coefficient Implementation in C++”


  • Manasi Chalam_599

    import math
    n=int(input())
    r=int(input())
    s=(math.factorial(n))/((math.factorial(r))*(math.factorial(n-r)))
    print(s)
    //python