Check for Children-Sum property in Binary Tree

March 24, 2025

Check for Children-sum property in binary tree

In this article, we will learn the approach and code about how to check for the children-sum property in binary tree in C++. Children sum property is true if the sum of the value of left node and right node is equal to the parent node value.

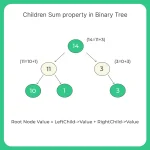
Check for children sum property in binary tree in C++

As an Input We are Given a tree and we have to check for children sum property. Whether that property if followed in an entire tree or not.

Note:-  Deviation of even single Node from above property will result in a negative answer.

Children-Sum Property:–

This property says that for each node sum of its left and right children should be equal to node value.

Also, following assumptions are to be kept in mind while recursively traversing tree

  1. A leaf node satisfies children sum property because leaf nodes don’t have any child nodes.
  2. An Empty tree satisfies Children sum property.

Algorithm:-

Step1:- Traverse the tree.
Step 2:- For every node in tree check whether the value in root node equals the sum of it lchild and rchild.

If yes continue from Step 1 Untill root==NULL

If No return false

The time complexity for above program is O(n). Since each node is covered once.

Find the size of binary tree

Find maximum in binary tree

Level Order Traversal LIne by Line

Check If binary tree if Foldable or not

check whether tree is Symmetric

Code Implementation to check for Children-sum property in binary tree in C++

Run 
#include<bits/stdc++.h>
using namespace std;
struct Treenode
{
  int val;
  Treenode *lchild;
  Treenode *rchild;
};

struct Treenode *newNode (int key)
{		
  struct Treenode *newnode = (struct Treenode *) malloc (sizeof (struct Treenode));
  newnode->val = key;
  newnode->lchild = NULL;
  newnode->rchild = NULL;
  return (newnode);
}

int TreefollowingChildSumProperty (Treenode * head)
{
  int lchild_val = 0, rchild_val = 0;
  if (head == NULL || (head->lchild == NULL && head->rchild == NULL))
    return 1;
  else
    {
      if (head->lchild != NULL)
        lchild_val = head->lchild->val;
      if (head->rchild != NULL)
        rchild_val = head->rchild->val;
      if ((head->val == lchild_val + rchild_val) && TreefollowingChildSumProperty (head->lchild) && TreefollowingChildSumProperty (head->rchild))
	    return 1;
      else
	    return 0;
    }
}

int main ()
{
  Treenode *root1 = newNode (232);
  Treenode *root2 = newNode (232);
  root1->lchild = newNode (231);
  root1->rchild = newNode (231);
  root1->lchild->lchild = newNode (431);
  root1->lchild->rchild = newNode (531);

  if (TreefollowingChildSumProperty (root1))
    cout << "Given Tree Follows children Sum Property\n";
  else
    cout << "Tree does not follows Children Sum property\n";

  getchar ();
  return 0;
}


Output:
Tree does not follows Children Sum Property