Triplet that sum to a given value in C
Triplet that sum to a given value
On this page we will discuss about triplet that sum to a given value in C. Given an array and a value, find if there is a triplet in array whose sum is equal to the given value. If there is such a triplet present in array, then print the triplet and return true. Else return false.

Triplet that Sum to Given Value in C
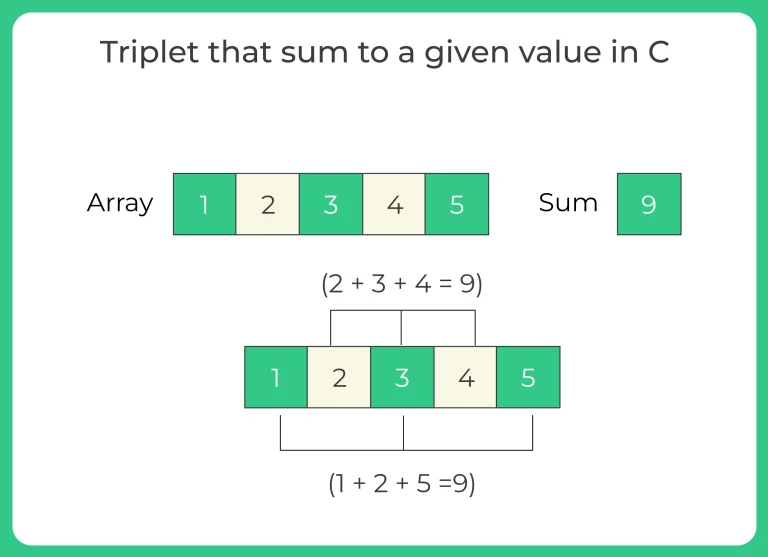
A triplet that sums to a given value C is a set of three elements in an array whose sum is equal to C. For example, if we have an array [1, 2, 3, 4, 5] and the target sum C is 9, then the triplet that sums to C is (2, 3, 4) because 2 + 3 + 4 = 9.
In general, given an array of n elements and a target sum C, the problem is to find all triplets (a, b, c) in the array such that a + b + c = C. The triplets may or may not be unique, and the order of the elements in each triplet does not matter.
On this page we will discuss two different methods for this-
- Naive Approach
- Sorting Approach
- Naive approach: Naive approach uses a nested loop to check all possible subarrays of the given array. For each starting index i, it checks all subarrays starting from i and ending at j, and calculates their sum. If the sum is equal to the given sum, it prints the indices of the subarray and returns. If no subarray is found, it prints a message indicating that no subarray was found.
Algorithm:
- Take size of the array from the user and store it in a variable say n.
- Now take n elements of the array from the user.
- Take one more interger value o
- Create three nested loop first loop runs from start to end (loop counter i), the second loop runs from i+1 to end (loop counter j) and the third loop runs from j+1 to end (loop counter k)
- The counter of these loops represents the index of 3 elements of the triplets.
- Find the sum of the ith, jth and kth element. If the sum is equal to a given sum. Print the triplet and break.
- If there is no triplet, then print “No triplet exists”.
C Code for naive approach
#include <stdio.h>
void findTriplets (int arr[], int n, int C)
{
for (int i = 0; i < n - 2; i++)
{
for (int j = i + 1; j < n - 1; j++)
{
for (int k = j + 1; k < n; k++)
{
if (arr[i] + arr[j] + arr[k] == C)
{
printf ("(%d, %d, %d)\n", arr[i], arr[j], arr[k]);
}
}
}
}
}
int main ()
{
int arr[] = { 1, 2, 3, 4, 5 };
printf ("Array: ");
int n = sizeof (arr) / sizeof (arr[0]);
for (int i = 0; i < n; i++)
{
printf ("%d ", arr[i]);
}
int sum = 9;
printf ("\nsum: %d", sum);
printf ("\nTriplets:\n");
findTriplets (arr, n, sum);
return 0;
}
Output
Array: 1 2 3 4 5 sum: 9 Triplets: (1, 3, 5) (2, 3, 4)
- sorting approach: The sorting approach involves sorting the given array and then using two pointers to find triplets that sum to the given value C. This approach has a time complexity of O(n^2), where n is the size of the array.
Algorithm:
- sort the array arr in ascending order
- for i = 0 to n-2:
- j = i+1
- k = n-1
- while j < k:
- if arr[i] + arr[j] + arr[k] == C:
- print (arr[i], arr[j], arr[k])
- j = j+1
- k = k-1
- else if arr[i] + arr[j] + arr[k] < C:
- j = j+1
- else:
- k = k-1
C Code for sorting approach
#include <stdio.h>
void sort (int arr[], int n)
{
int i, element, j;
for (i = 1; i < n; i++) { element = arr[i]; j = i - 1; while (j >= 0 && arr[j] > element)
{
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = element;
}
}
void findTriplets (int arr[], int n, int sum)
{
sort (arr, n);
for (int i = 0; i < n - 2; i++)
{
int j = i + 1;
int k = n - 1;
while (j < k)
{
if (arr[i] + arr[j] + arr[k] == sum)
{
printf ("(%d, %d, %d)\n", arr[i], arr[j], arr[k]);
j++;
k--;
}
else if (arr[i] + arr[j] + arr[k] < sum)
{
j++;
}
else
{
k--;
}
}
}
}
int main ()
{
int arr[] = { 1, 2, 3, 4, 5 };
printf ("Array: ");
int n = sizeof (arr) / sizeof (arr[0]);
for (int i = 0; i < n; i++)
{
printf ("%d ", arr[i]);
}
int sum = 9;
printf ("\nsum: %d", sum);
printf ("\nTriplets:\n");
findTriplets (arr, n, sum);
return 0;
}
Output
Array: 1 2 3 4 5 sum: 9 Triplets: (1, 3, 5) (2, 3, 4)



Login/Signup to comment